Купец выехал из а в в имея 100 золотых на дороге разбойники грабят проезжающих разбирают тот процент от имеющийся в данный момент суммы который указан на схеме какое максимальное количество золотых может купец в

👇

Ответ:

TuplinaTina

04.02.2023

Если он поедет через пункт С
1) 100*30:100=30 монет- заберут по пути в С
2) 100-30=70 останется
3) 70*30:100=21 монету заберут по пути в В
4) 70-21=49 монет он привезет в пункт В

Если он поедет через пункт D
1) 100*4:100= 4 монеты заберут по пути в D
2) 100-4=96 монет останется
3) 96*50:100=48 монет заберут по пути в В
4) 96-48=48 монет он привезёт в пункт В
ответ: Максимальное количество монет может привезти купец в пункт В=49 монет

4,5(33 оценок)

Открыть все ответы

Ответ:

Bublick08

04.02.2023

просто подряд подставлять целые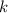

при 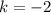k=-2 имеем корни

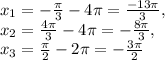
$x_1=-\frac{\pi}{3}-4\pi=\frac{-13\pi}{3},\\x_2=\frac{4\pi}{3}-4\pi=-\frac{8\pi}{3},\\x_3=\frac{\pi}{2}-2\pi=-\frac{3\pi}{2}$

Первые два в промежуток не попадают, третий - попадает.

при 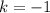k=-1 имеем корни

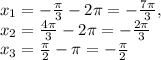$x_1=-\frac{\pi}{3}-2\pi=-\frac{7\pi}{3},\\x_2=\frac{4\pi}{3}-2\pi=-\frac{2\pi}{3}\\x_3=\frac{\pi}{2}-\pi=-\frac{\pi}{2}$ ,

первый корень в промежуток не попадает, другие два - попадают.

Если подставлять 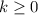$k\geq 0$ , то увидим, что полученные в итоге корни уже не будут вписываться в границы отрезка.

универсальный, но не очень удобный): оценить и проверить, при каких целых 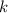неравенство 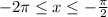$-2\pi\leq x\leq -\frac{\pi}{2}$ имеет решение. Для этого все серии корней по отдельности подставляем вместо :

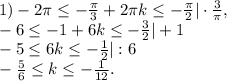
$1) -2\pi\leq -\frac{\pi}{3}+2\pi k\leq -\frac{\pi}{2} |\cdot\frac{3}{\pi} ,\\-6\leq -1+6k \leq -\frac{3}{2}|+1\\-5\leq 6k\leq -\frac{1}{2} |:6\\-\frac{5}{6}\leq k\leq -\frac{1}{12}.$

Очевидно, что целых 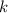, удовлетворяющих последнему неравенству, не существует. Т.е. ни один из корней этой серии промежутку не принадлежит.

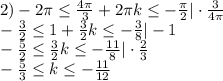
$2) -2\pi\leq \frac{4\pi}{3}+2\pi k \leq -\frac{\pi}{2}|\cdot\frac{3}{4\pi}\\ -\frac{3}{2} \leq 1+\frac{3}{2}k\leq -\frac{3}{8}|-1\\-\frac{5}{2}\leq \frac{3}{2}k\leq -\frac{11}{8}|\cdot\frac{2}{3}\\-\frac{5}{3}\leq k\leq -\frac{11}{12}$

Последнему неравенству удовлетворяет только одно целое 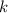- 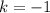k=-1 . Корень находим при подстановке значения 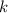в соответствующую серию.

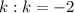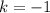То же можно проделать с третьей серией и убедиться, что неравенство удовлетворяют только 2 значения k: k=-2 и k=-1 . Их также подставляем в соответствующую серию и находим корни.