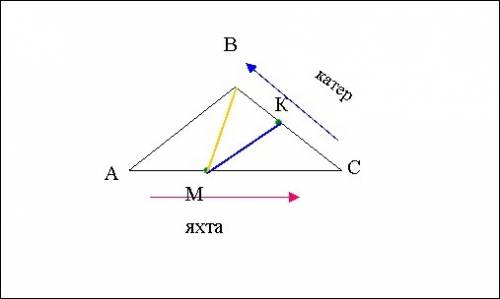
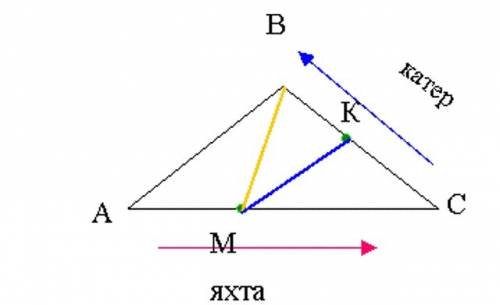
Чертёж ниже, кликни по нему мышкой.
Яхта села на мель в точке М, поэтому будем искать расстояние ВМ, которое пройдёт лодка к яхте и расстояние КМ, которое пройдёт катер к яхте.
1). Будем находить длины сторон треугольников по теореме косинусов, поэтому сначала из ∆АВС найдём cos<C
АВ2 = ВС2 + АС2 - 2*ВС*АС*cos<C
отсюда
cos<C = (ВС2 + АС2 - АВ2)/(2*ВС*АС)
cos<C = (702 + 902 - 702)/(2*70*90)=
= 8100/12600 = 81/126 = 9/14
cos<C = 9/14
2) АМ = СК = 10 * 2 = 20 км
МС = АС - АМ = 90 - 20 = 70 км
3) Из ∆МКС найдём длину стороны КМ по т. косинусов
КМ2 = МС2 + СК2 - 2*МС*СК*cos<C
КМ2 = 702 + 202 - 2 * 70 * 20 * 9/14 = 4900 + 400 - 1800 = 3500
КМ = √3500 = 10√35 км
4) Из ∆МВС найдём длину стороны ВМ:
ВМ2 = МС2 + СВ2 - 2*МС*СВ*cos<C
ВМ2 = 702 + 702 - 2 * 70 * 70 * 9/14 = 9800 - 9800 * 9/14 =
= 9800 - 9800 * 9/14 = 9800 - 6300 = 3500
ВМ = √3500 = 10√35 км
5) Расстояния ВМ, которое пройдёт лодка для оказания и расстояние КМ, которое пройдёт катер для оказания яхте равны между собой: ВМ = КМ = 10√35 км.
Скорости тоже равны по 20км/ч
Значит, и время будет одинаковое, 10√35 км : 20 км/ч = √35/2 ч ≈ 2,9ч, т.е. лодка и катер к яхте прибудут одновременно.
ответ: лодка и катер к яхте прибудут одновременно.
Сначала без х:
Площадь 1-го отреза: 18м·0,75м = 13,5м²
Площадь одной наволочки: 13,5м²:15 = 0,9м²
Площадь 22 наволочек: 0,9м²·22 = 19,8м²
Длина 2-го отреза: 19,8м²:1,2м = 16,5м
Теперь с х:
Пусть х - длина 2-го отреза, тогда площадь 2-го отреза 1,2х. Площадь одной наволочки: 1,2х: 22. Площадь наволочки, получаемая из 1-го отреза записывается выражением: 18·0,75:15.
Уравнение:
1,2х:22 = 18·0,75:15
По основному свойству пропорции:
1,2х·15 = 22 ·18·0,75
18х = 18·16,5
х = 16,5
ответ: длина 2-го отреза 16,5м