Решите уравнения : 1) (3.9-х) : 4 = 0.7 2)6*(x+1.5)=25.2

👇

Увидеть ответ

Ответ:

Элис6666666666

14.11.2022

1)(3,9-х):4=0,7
3,9-х=2,8
х=3,9-2,8
х=1.1
2)6*(х+1,5)=25,2
х+1,5=4,2
х=4,2-1,5
х=2,7

4,6(92 оценок)

Открыть все ответы

Ответ:

Aizere1111

14.11.2022

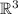Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода 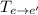$T_{e \rightarrow e'}$ можно найти следующим образом:

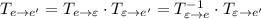
$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

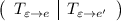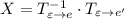
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

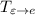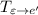Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

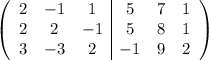
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

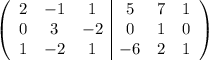
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

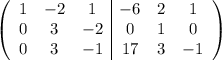
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

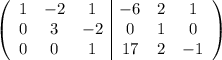
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

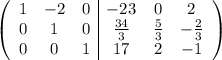
$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

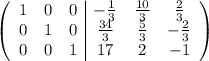
$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

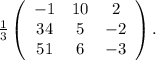
$\frac{1}{3}\left(\begin{array}{ccc}-1&10&2\\34&5&-2\\51&6&-3\end{array}\right).$

4,8(27 оценок)

Ответ:

juliagolub2015

14.11.2022

$y=4\, cos^2(x-7)$

область определения функции cos - всё множество действительных чисел, а вот множество значений этой функции (вне зависимости, какой аргумент будет записан) - это отрезок от (-1) до (+1) .

$-1\leq cosx\leq 1\; \; \rightarrow \; \; \; cosx\in [-1,1\, -1\leq cos(x-7)\leq 1$