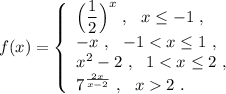
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
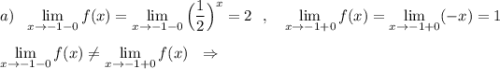
При х= -1 функция имеет разрыв 1 рода .
При х=1 функция непрерывна.
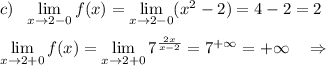
При х=5 функция имеет разрыв 2 рода .
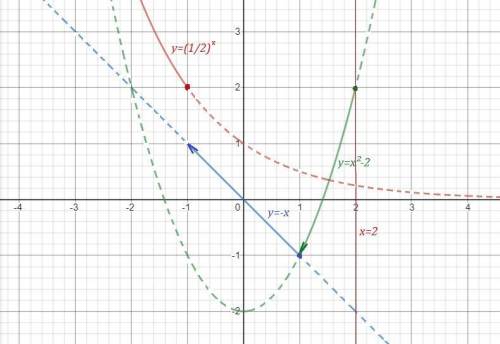
График функции нарисован сплошными линиями.
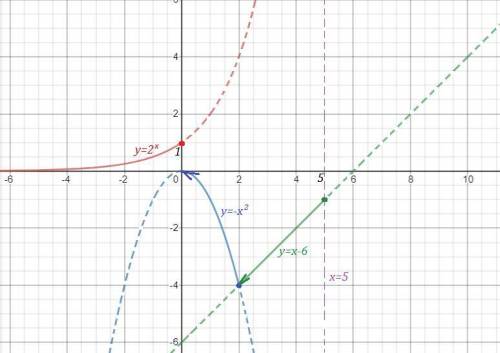
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
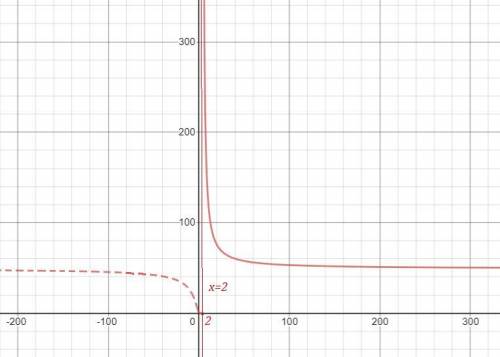
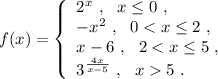
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
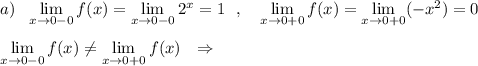
При х=0 функция имеет разрыв 1 рода .
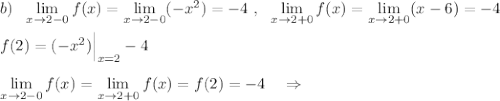
При х=2 функция непрерывна.
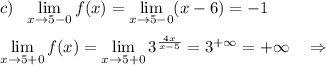
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
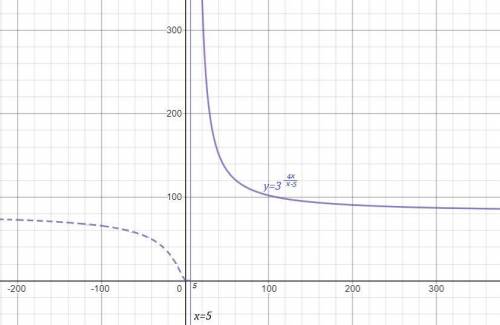
На 1 рисунке нет чертежа функции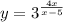 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
сначала ищем иксы
(1-х)(х-2)=0
1-х=0, х₁=1
х-2=0, х₂=2
отметим их на координатной прямой, получим 3 промежутка:
(-∞; 1); (1;2); (2; +∞)
₀₀>х
1 2
для того, чтобы узнать знаки в промежутках нужно в уравнение подставить числа из этих промежутков, например:
(2;+∞): (1-3)(3-2) = -2*1 = -2 < 0 (ставим -)
(1;2): (1-1,5)(1,5-2) = -0,5*(-0,5) = 0,25 > 0 (cтавим +)
(-∞; 1): (1-0)(0-2) = 1*(-2) = -2 < 0 (ставим -)
- + -
₀₀>x
1 2
возвращаемся к неравенству, у нас должно быть < 0, а это два крайних промежутка
ответ: (-∞; 1)∪(2; +∞)