1. чтобы понять, проходит ли график функции через точку А (3, 23), надо подставить координаты точки в функцию y = х²+ 7х-1
3² + 7 * 3 - 1 = 23
9 +20 = 23
29 ≠ 23, значит график не проходит через данную точку
2. формулы координаты вершины параболы: х = -b/2a, y = (4ac - b²)/4a
у = х²-6х + 4
найдем координаты вершины: х = 6/2 = 3
у = (4*4 - 36)/4 = -20/4 = -5
3. у = х²-2х + 8
если график функции пересекается с осью ОY, то в этой точке х = 0
у = 0² - 2*0 + 8 = 8
(0; 8) - точка пересечения графика с осью ОY
4. у = х²-7х +6
если график функции пересекается с осью ОХ, то в этой точке у = 0
х²-7х +6 = 0
х = 1, х = 6
(1; 0), (6; 0) - точки пересечения графика с осью ОХ
t≤2, t≥3
Объяснение:
все выражение находится под корнем. Корень имеет смысл, когда подкоренное выражение больше или равно нулю:
t²-5t+6≥0
найдем корни квадратного трехчлена, для этого приравняем его к нулю:
t²-5t+6=0
по теореме Виета: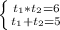 
, откуда корни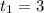 
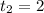
отметим точки на прямой (рис) (закрашенными, т.к наше неравенство нестрогое)
знаки начинаются с +, дальше чередуем.
у нас ≥, выбираем +
t ∈ (-∞; 2] ∪ [3; +∞), что можно понимать, как: нас устраивает t меньше 2 и 2 включительно и больше 3, включая 3 => t≤2, t≥3
4х^2-2х-2х-1-4х^2-12x-9=38
4х^2 сокращается
-16х-10=38
Переносим с х в одну часть , без х в другую
-16х=38+10
-16х=48
х=48:(-16)
х=-3