Объяснение:Найти производную следующих функций:
1) у = 4х^4 + 3х; y'= (4x⁴+3x)'= 16x³+3
2) у = 12х^2 - х – 2; y'= (12x²-x-2)' =24x - 1
3) у = -4х^9 - 8х^4 – 6х + 22; y' = (-4x⁹-8x⁴-6x+22)= - 36x⁸-32x³-6
4) у= 8х^7 - 14х^5 + 5х - 10; y' =(8x⁷-14x⁵+5x-10)'= 56x⁶-70x⁴+5
5) у = 6х^3 + (1/9)х^3 + 9х; y'= 18x²+(1/3)x²+9
6) у = 19х^4 + 3х^8 – 22. y'=76x³+24x⁷
«Производная степенной, логарифмической и показательной функций»
Найти производную следующих функций:
1. у = (х - 2)^8 y' = 8(x-2)⁷(x-2)'=8(x-2)⁷
2. у = (х2 + 2х)^3 y'= 3(x²+2x)²(x²+2x)'= 3(x²+2x)(x+2)=3x(x+2)²= 3x(x²+4x+4)=3x³+12x²+12x
3. у = (х +3)^4 y'=4(x+3)³(x+3)'= 4(x+3)³ =4( x³+9x²+27x+27)
4. у = 41^х y' = 41ˣ ln41
5. у = (3 + 5х + х3)^2 y' = 2( x³+5x+3)( x³+5x+3)'= 2( x³+5x+3)(2x+5)
Во-первых, отметим, что аргументы логарифмов должны быть строго больше нуля, но поскольку аргументы -- целые числа, то они должны быть хотя бы 
. С другой стороны, как нетрудно заметить, их сумма равна 
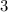. Стало быть, каждый из них равен единице: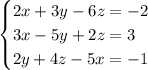 
Детерминант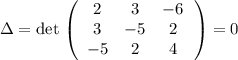 
(-(1 строка) - (2 строка) = (3 строка)). Решение можно параметризовать: 
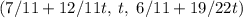, откуда 
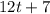должно делиться на 
, а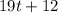 
должно делиться на 
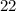. Тогда 
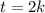, потому 
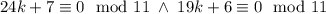. Из первого 
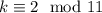, а из второго -- 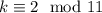. Итак, 
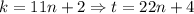, поэтому решение переписывается в виде 
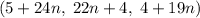. Итак, слева у исходного неравенства стоит нуль, а справа -- 
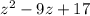. Получаем, что 
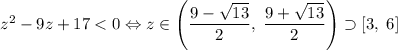, а потому подходит только 
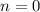и соответствующая тройка 
.
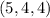