Алгебра: Решите неравенство 5 в степени 6х-3 125в степени х+2

Решите неравенство 5 в степени 6х-3> 125в степени х+2

👇

Увидеть ответ

Ответ:

сергей4995258

05.10.2021

Решение на фото.....
Решите неравенство 5 в степени 6х-3> 125в степени х+2

4,8(22 оценок)

Открыть все ответы

Ответ:

Donziik

05.10.2021

Объяснение:

Для решения всех трех задач применяем правило нахождения геометрической вероятности: Если фигура F₁ содержится в фигуре F, тогда вероятность попадания в фигуру F₁, при условии попадания в фигуру F равна отношению площадей: Р=S(F₁):S(F)

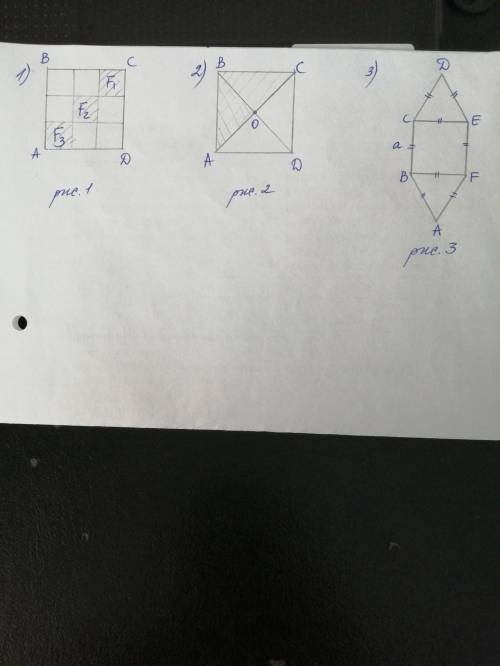
Задача 1 (рис.1)

Квадрат ABCD разбит на 9 квадратиков одинаковой площади. Площадь каждого такого квадратика равна 1/9 от площади квадрата АВСD. Попадание в каждый из этих квадратиков (в том числе и в F₁ - правый верхний, F₂ - центральный и F₃ - левый квадратики) равновероятно и по правилу нахождения геометрической вероятности составляет

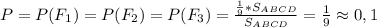
$P=P(F_1)=P(F_2)=P(F_3)=\frac{\frac{1}{9}*S_{ABCD}}{S_{ABCD}}=\frac{1}{9}\approx0,1$

Задача 2 (рис.2)

Площадь треугольника АВС составляет половину площади квадрата АВСD, поэтому, вероятность попадания в треугольник АВС по правилу нахождения геометрической вероятности равна:

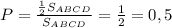
$P=\frac{\frac{1}{2}S_{ABCD}}{S_{ABCD}}=\frac{1}{2}=0,5$

Площадь треугольника АОВ составляет четверть площади квадрата АВСD, поэтому, вероятность попадания в треугольник АОВ по правилу нахождения геометрической вероятности равна:

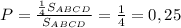
$P=\frac{\frac{1}{4}S_{ABCD}}{S_{ABCD}}=\frac{1}{4}=0,25$

Задача 3 (рис.3)

Площадь фигуры ADCDEF состоит из суммы площадей квадрата BCED и площадей равносторонних (и равных друг другу) треугольников BAF и CDE.

Пусть сторона квадрата и треугольника равна а, тогда

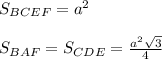
$S_{BCEF}=a^2\\\\S_{BAF}=S_{CDE}=\frac{a^2\sqrt{3}}{4}$

Площадь фигуры ABCDEF равна

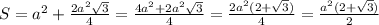
$S=a^2+\frac{2a^2\sqrt{3}}{4}=\frac{4a^2+2a^2\sqrt{3}}{4}=\frac{2a^2(2+\sqrt{3})}{4}=\frac{a^2(2+\sqrt{3})}{2}$

Итак, вероятность попадания в квадрат BCEF по правилу нахождения геометрической вероятности равно отношению площади квадрата BCEF к площади фигуры ADCDEF и составляет

$P=\frac{a^2}{\frac{a^2(2+\sqrt{3})}{2}}=\frac{2}{2+\sqrt{3}}\approx0,54$

а вероятность попадания в каждый из равносторонних треугольников BAF и CDE по правилу нахождения геометрической вероятности равно отношению площади треугольника к площади фигуры ADCDEF и составляет

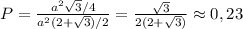
$P=\frac{a^2\sqrt{3}/4 }{a^2(2+\sqrt{3})/2}=\frac{\sqrt{3}}{2(2+\sqrt{3})} \approx0,23$