если a < 0, нет точек пересечения,
если а = 0, бесконечно много точек пересечения,
если а > 0. одна точка пересечения.
Объяснение:
Графический метод.
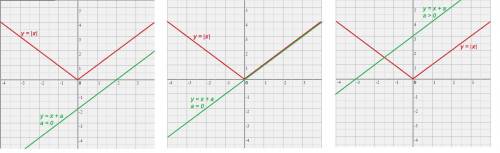
1) Построим график функции у = |x| (красный график)
Так как |x| = x при x ≥ 0, то для x ≥ 0 графиком является луч с началом в точке (0; 0), биссектриса первой координатной четверти.
Так как |x| = - x при x < 0, то для x < 0 графиком является часть прямой у = - х, расположенная во второй координатной четверти.
2) Построим график функции у = х + а (зеленый график) для различных значений а.
Графиком этой функции является прямая, проходящая под углом 45° к положительному направлению оси Ох, и пересекающая ось Оу в точке (0; а).
Если а < 0, то прямая проходит ниже графика функции у = |x| и не пересекает его.Если а = 0, то прямая проходит через начало координат и совпадает с частью графика функции y = |x|, тогда бесконечно много общих точек.Если а > 0, то прямая пересекает график функции y = |x| в одной точке.Аналитический метод:
1) a < 0
|x| = x + a
Если х ≥ 0, то x = x + a
a = 0
но а < 0, значит точек пересечения нет.
Если х < 0, то - x = x + a
- 2x = a
здесь левая часть положительна, правая - отрицательна, значит нет точек пересечения.
2) а = 0
|x| = x
равенство верно, для любых x ≥ 0.
Бесконечно много общих точек.
3) а > 0
Если x ≥ 0, то x = x + a
a = 0
но а > 0, значит точек пересечения нет.
Если x < 0, то - x = x + a
- 2x = a
обе части положительны, значит для каждого а > 0 найдется значение х, при котором равенство будет верно, следовательно одна точка пересечения.
У меня нет возможности крепить файлы - картинки. Поэтому попытаюсь без них.
1. Если учесть, что все боковые грани этой призмы - равные прямоугольники, то можно найти квадрат диагонали такого прямоугольника. В нем есть катет длиной 24см- сторона основания и второй катет длиной 12см- боковое ребро призмы.
24²+12²=576+144=720.
2. Что есть сечение? Равнобедренный треугольник. В нем боковые стороны - диагонали двух боковых граней, а основание - сторона верхнго основания. Найдем высоту в этом сечении. Это и медиана тоже, т.к. проведена к основанию треугольника.
итак, высота сечения √(720-(24/2)²)=√(720-144)=√576=24
3. Зная теперь половину основания, т.е. 24/2=12 /см/, а также высоту, проведенную к этому основанию, т.е. 24, найдем площадь сечения. ОНА равна 24*12=288/см²/
область зеачений это все те у
которые может принимать функция
можно сказать что обл.знач.
это высота функции
y= –x²+6x–5
y= –x²+6x–3²+3²–5
y= –(x²–6x+3²)+9–5
y= –(x–3)²+4
это парабола. ветви вниз
вершина на высоте 4
т.е. высота параболы от 4 до –∞