y=|x-2|-|x+1|
Разобьём числовую ось на три промежутка точками х=-1 и х=2.
---------------------[-1 ]--------------[ 2 ] --------------------
1) -∞<x≤-1 : (x-2)<0 ⇒|x-2|=-x+2 , (x+1)<0 ⇒ |x+1|=-x-1 ,
y=|x-2|-|x+1|=-x-2-(-x-1)=3
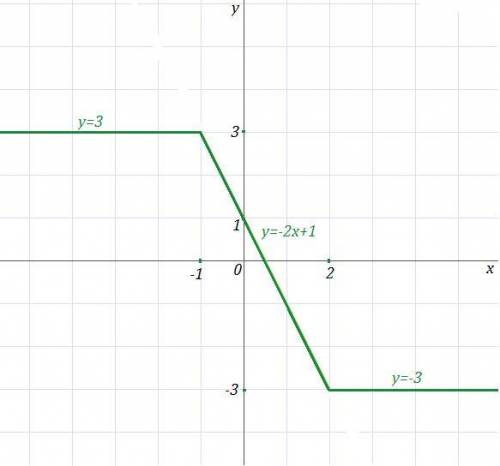
Строим на рассматриваемом промежутке прямую у=3 .
2) -1<x≤2 : (x-2)<0 ⇒ |x-2|=-x+2 , (x+1)>0 ⇒ |x+1|=x+1 ,
y=|x-2|-|x+1|=-x+2-(x+1)=-2x+1 .
Строим на промежутке (-1,2 ] прямую у= -2х+1 .
3) x>2 : (x+2)>0 ⇒ |x-2|=x-2 , (x+1)>0 ⇒ |x+1|=x+1 ,
y=|x-2|-|x+1|=x-2-(x+1)=-3 .
Строим при x>2 прямую у= -3 .
{ x1 + x2 = -b/a
{ x1*x2 = c/a
1) a + b + c = 0
1 + b/a + c/a = 0
1 + x1*x2 - (x1 + x2) = 0
x1*x2 - x1 - x2 + 1 = 0
(x1 - 1)*(x2 - 1) = 0
x1 = 1 или x2 = 1
Следствие: Если a + b + c = 0, то один из корней равен 1.
2) a + c = b
1 + c/a = b/a
1 + c/a - b/a = 0
1 + x1*x2 + x1 + x2 = 0
x1*(x2 + 1) + x2 + 1 = 0
(x1 + 1)(x2 + 1) = 0
x1 = -1 или x2 = -1
Следствие: Если a + c = b, то один из корней равен -1