the only thing that you have any questions please feel free contact us at our house in order for me to make this happen to make sure you have any questions or concerns you have a good idea to make sure you will be able to make this a good time for a great weekend as well as well but I am looking for a good day and time for me if you are doing good day please see the only one of our clients are saying I just want you have a good day I just want a good day please contact the only thing is I just want to i I just want a great day please see attached file is scanned image to be able to getting together.
Объяснение:
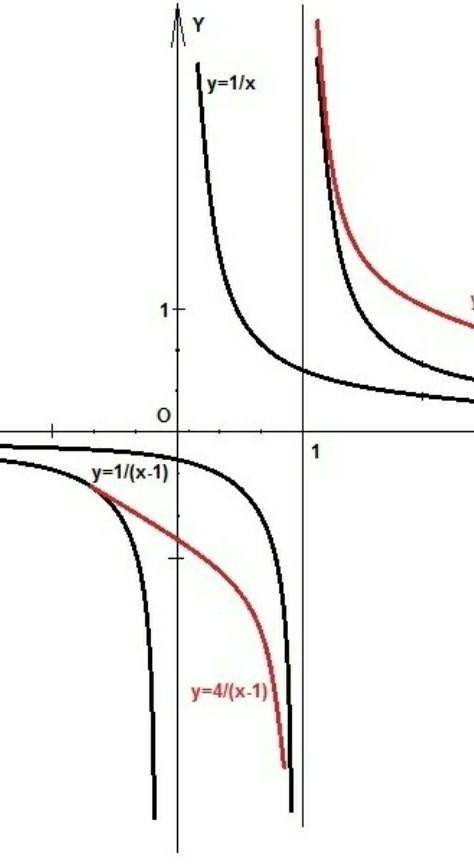
У нас есть график y = 1/x.
1) Чтобы получить y = 1/(x-1), его нужно сдвинуть на 1 вправо.
Теперь вертикальная линия разрыва будет x = 1, а не x = 0.
Чтобы получить y = 4/(x-1), нужно все значения умножить на 4.
2) Точно также, сначала сдвигаем график y = 1/x на 2 влево, а потом переворачиваем график и умножаем все значения на 3.
3) Тоже, сначала сдвигаем график y = 1/x на 1 вправо, потом умножаем все значения на 2, и, наконец, сдвигаем весь график на 3 вверх.
1 график я нарисовал на рисунке, остальные делаются точно также.
Но это очень приблизительный график, точнее в Пайнте не построишь.
Главное, понятен порядок построения.
При x < -2 будет |x+2| = -x-2; |x| = -x
-x - 2 - x(-x) <= 0
x^2 - x - 2 <= 0
(x + 1)(x - 2) <= 0
Решение неравенства: x ∈ [-1; 2]
Но по условию x < -2, поэтому на этом промежутке решений нет.
При x ∈ [-2; 0) будет |x+2| = x+2; |x| = -x
x + 2 - x(-x) <= 0
x^2 + x + 2 <= 0
Выделим полный квадрат
x^2 + 2*x*1/2 + (1/2)^2 - (1/2)^2 + 2 <= 0
(x + 1/2)^2 + 7/4 <= 0
Сумма двух неотрицательных чисел не может быть не положительной.
На этом промежутке решений тоже нет.
При x >= 0 будет |x+2| = x+2; |x| = x
x + 2 - x*x <= 0
-x^2 + x + 2 <= 0
Поменяем знаки в левой части, тогда поменяется и знак неравенства.
x^2 - x - 2 >= 0
(x + 1)(x - 2) >= 0
Решение неравенства: x ∈ (-oo; -1] U [2; +oo)
Но по условию x >= 0
ответ: x ∈ [2; +oo)
2) 3x - |x+10| - |2-x| <= -6
Тут тоже две особые точки: x = -1 и x = 2
При x < -10 будет |x+10| = -x-10; |2-x| = 2-x
3x - (-x - 10) - (2 - x) <= -6
3x + x + 10 - 2 + x + 6 <= 0
5x + 14 <= 0
x <= -14/5 = -2 4/5
Но по условию x < -10
Решение: x < -10
При x ∈ [-10; 2) будет |x+10| = x +10; |2-x| = 2-x
3x - (x+10) - (2-x) <= -6
3x - x - 10 - 2 + x + 6 <= 0
3x - 6 <= 0
x <= 6/3 = 2
Но по условию x ∈ [-10; 2)
Решение: x ∈ [-10; 2)
При x >= 2 будет |x+10| = x+10; |2-x| = x-2
3x - (x+10) - (x-2) <= -6
3x - x - 10 - x + 2 + 6 <= 0
x - 2 <= 0
x <= 2
Но по условию x >= 2
Решение: x = 2.
ответ: x ∈ (-oo; 2]
3) 25x^2 - 4|8-5x| <= 80x - 64
Здесь одна особая точка x = 5/8.
При x < 5/8 будет |8-5x| = 8-5x
25x^2 - 4(8-5x) <= 80x - 64
25x^2 - 32 + 20x - 80x + 64 <= 0
25x^2 - 60x + 32 <= 0
D/4 = 30^2 - 25*32 = 900 - 800 = 100 = 10^2
x1 = (30 - 10)/25 = 20/25 = 4/5
x2 = (30 + 10)/25 = 40/25 = 8/5
(5x - 4)(5x - 8) <= 0
x ∈ [4/5; 8/5]
По условию x < 8/5
Решение: x ∈ [4/5; 8/5)
При x >= 8/5 будет |8-5x| = 5x-8
25x^2 - 4(5x-8) <= 80x - 64
25x^2 - 20x + 32 - 80x + 64 <= 0
25x^2 - 100x + 96 <= 0
D/4 = 50^2 - 25*96 = 2500 - 2400 = 100 = 10^2
x1 = (50 - 10)/25 = 40/25 = 8/5
x2 = (50 + 10)/25 = 60/25 = 12/5
x ∈ [8/5; 12/5]
По условию x >= 8/5
Решение: x ∈ [8/5; 12/5]
ответ: x ∈ [4/5; 12/5]