a) D(x) = (-∞; +∞)
б) D(x) = (-∞;0) U (0;+∞)
Объяснение:
Область определения функции - это те значения аргумента (х), при которых СУЩЕСТВУЕТ функция.
Другими словами, если вы хотите найти область определения функции, то это значит найти значения х.
В наших случаях:
а)
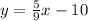
Это линейная функция. Аргумент (х) не имеет ограничений (не стоит в знаменателе , под знаком корня).
Поэтому : x - любое число, или
D(x) = (-∞; +∞)
б)
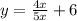
В этой функции мы видим х в знаменателе. Значит функция будет существовать при всех значениях аргумента (х), кроме 0, т.е
5х≠0
х≠0
получаем:
D(x) = (-∞;0) U (0;+∞)
Объяснение:
Показательной функцией назыввается функция вида y = ax, где a > 0 и a ≠ 1. График функции имеет следующий вид: Рассмотрим свойства функции: Областью определения функции является множество всех действительных чисел R. Множеством значений функции являются все положительные числа, т. е. промежуток E(y): (0; +∞). Наименьшего и наибольшего значений функция не имеет. Функция не является ни нечетной, ни четной.Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
2. область значения х∈[12,+∞)
3. нули функции: х=0 => y=12+5^(2/3), y≠0
4. у(х) - всегда положительна
5. монотонность: производная функции y'=2/3 (x-5)^(1/3), т.е. до 5 функция отрицательна (убывает), после 5 - возрастает
6. точки экстремума: х=5 - в этой точке минимум функции
7. функция не является ни четной ни нечетной т.к. не выполняются условия у(-х)=у(х), у(-х)=-у(х)
8. функция не является периодической, т.к. не выполняется условие у(х+Т)=у(х)