По определению, arcsin 4/5 - это угол α, синус которого равен 4/5.
Причем, это угол, принадлежащий интервалу [- π/2; π/2].
Т.е.
arcsin 4/5 = α, sinα = 4/5, α ∈ [- π/2; π/2].
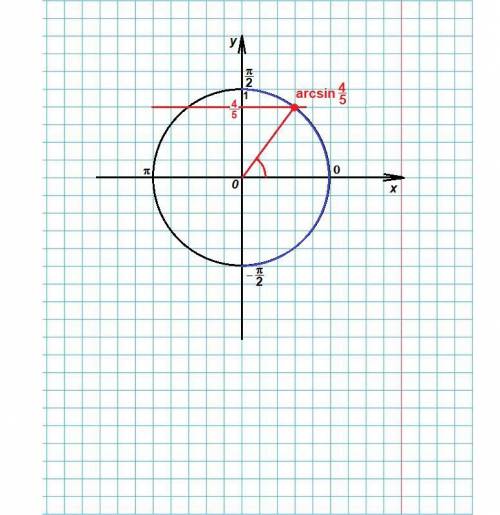
Построим этот угол на тригонометрической окружности.
Так как синус угла α - это ордината (координата у) точки, повернутой на угол α, то значение синуса 4/5 отмечаем на оси Оу.
Радиус окружности равен 1, поэтому делим его на 5 частей и отмечаем 4 из них.
Через полученную на оси Оу точку проводим горизонтальную прямую. Точка пересечения этой прямой с правой полуокружностью (с синей) и есть точка, соответствующая углу поворота α = arcsin 4/5.
v = t^2 - 8t + 2
s = t^3/3 - 4t^2 + 2t
2) Решение точно такое же
v = 6t^2 - 10t
s = 2t^3 - 5t^2
Путь, пройденный за третью секунду
S = s(3) - s(2) = 2*3^3 - 5*3^2 - 2*2^3 + 5*2^2 = 54 - 45 - 16 + 20 = 13 м.
3) Вот рисунок.
Найдем границы участка.
x = 5 - x; x = 2,5, y = 2,5
x = 1; y = 5 - x = 5 - 1 = 4
x = 2; y = 5 - x = 5 - 2 = 3
A(1; 4); B(1; 1); C(2; 2); D(2; 3)