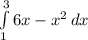 =|3,1(3x^2-x^3/3)=3*3^2-3^3/3-3+1/3=27-9-3+1/3=15+1/3=46/3
=|3,1(3x^2-x^3/3)=3*3^2-3^3/3-3+1/3=27-9-3+1/3=15+1/3=46/3
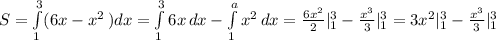
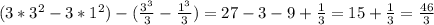
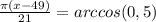
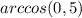 , получая
, получая 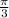 :
: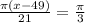
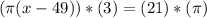
 :
: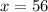
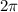 и определим решение в четвертом квадранте:
и определим решение в четвертом квадранте: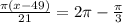
 :
: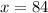
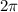 из 84, пока угол не упадет между 0 и
из 84, пока угол не упадет между 0 и 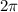 . В этом случае
. В этом случае 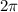 нужно вычесть 13 раз:
нужно вычесть 13 раз: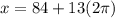
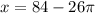
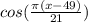 равен 42, то есть значения будут повторяться через каждые 42 радиан в обоих направлениях:
равен 42, то есть значения будут повторяться через каждые 42 радиан в обоих направлениях: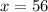 ±
±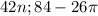 ±
±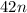 .
.