Докажем тождество:
(tga – sina) * (cos^2 a/sina+ctga) = sin^2 a;
Раскроем скобки в левой части тождества и тогда получим:
tga * cos^2 a/sina + tga * ctg a – sin a * cos^2 a/sina – sina * ctga = sin^2 a;
Используя основные тождества тригонометрии, упростим правую часть выражения.
Получаем:
sina/cosa * cos^2 a/sina + 1 – sina * cos^2 a/sina – sina * cosa/sina = sin^2 a;
Сократи дроби и останется:
1/1 * cosa/1 + 1 – 1 * cos^2 a/1 – 1 * cosa/1 = sin^2 a;
cos a + 1 – cos^2 a – cos a = sin^2 a;
1 – cos^2 a = sin^2 a;
sin^2 a = sin^2 a;
Тождество верно.
х = 16; y = 11
Объяснение:
ваш пример очень простой, видимо чтобы понять азы, так что вникайте!
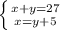
сложим уравнения из данной системы друг с другом:
(x+y) + x = 27 + (y+5)
раскроем скобочки и приведём подобные члены
х + y + x = 27 + y + 5
2х + y = 32 + y
перенесём все неизвестные в правую часть
2х + y - y = 32
снова образовались подобные члены, это "y" и в данном случае, т.к. у них разные знаки, они взаимоуничтожаются
2х = 32
x = 32:2
x = 16
Подставим найденный икс (x) в любое уравнение системы чтобы найти игрек (y)
например в:
x + y = 27
16+y=27
y = 27 - 16
y = 11
3^(2x)-2^y=(3^x-√2^y)(3^x+√2^y)=25(3^x+√2^y)
25(3^x+√2^y)=725
3^x+√2^y=29
3^x - √2^y = 25 складываем
2*3^x=54
3^x=27
x=3
3^2+√2^y=29
√2^y=2
2^y=4
y=2
ответ (3 2)
Вторая система:{6^x-2*3^y=2{6^x*3^y=12
6^x=2+2*3^y
2(1+3^y)*3^y=12
3^y=t t>0
t(t+1)=6
t²+t-6=0
D=1+24=25
t12=(-1+-5)/2=2 -3
-3 нет t>0
3^y=2
y=log₃ 2
6^x*3^log₃ 2 = 12
6^x=6
x=1
ответ ( 1 log₃ 2)