а) n-ый член геометрической прогрессии ищется по формуле:
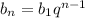
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
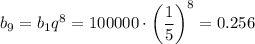
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
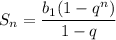
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
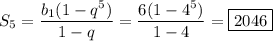
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
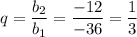
Сумма бесконечно уб. г.п. 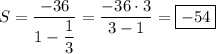
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
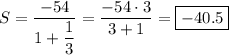
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
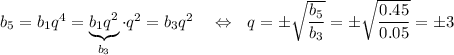
Так как по условию q>0, то q=3
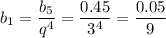
Сумма первых восьми членов этой прогрессии равна:

у=х-4 и y=x+3, графики этих функций параллельны, а система этих уравнений не имеет решений.
Объяснение:
К данному уравнению x−y=4 выбери из предложенных уравнений второе уравнение так, чтобы полученная система не имела решений:
ответ (можно получить, используя построение):
2x−y=5
y+x=−4
y=x+3
Можно не использовать построение, а ответ получить, опираясь на знания)
Для начала все уравнения запишем в виде уравнений функций:
x−y=4 2x−y=5 y+x=−4 y=x+3
-у=4-х -у=5-2х у= -4-х
у=х-4 у=2х-5 у= -х-4
Известно, что система не имеет решений, если графики функций, выраженных этими уравнениями, параллельны.
Известно также, что графики линейных функций параллельны при одинаковых коэффициентах при х.
Смотрим на коэффициенты при х.
у=х-4 и y=x+3, графики этих функций параллельны, а система этих уравнений не имеет решений.