Ч.т.д.
_________
- двойной факториал: произведение всех натуральных чисел отрезка [1;x] четности, совпадающей с четностью x.
Свойство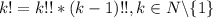 
очевидно (k и k-1 - последовательные натуральные числа, а значит они имеют разную четность, а значит один из сомножителей содержит все четные числа, а 2ой - все нечетные из отрезка [1;k], т.е. их произведение содержит все натуральные числа отрезка [1;k] по одному разу. А это и есть 
)
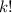Пояснение к преобразованию : в этом выражении содержится произведение всех четных чисел отрезка [1;2n] , всего этих сомножителей
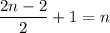, причем k-ый из них представим в виде 
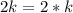. А тогда, вынеся из каждого сомножителя 2, и получим представление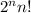 
4²⁷; 3³⁶; 2⁴⁵; 5¹⁸;
Объяснение:
а = 2⁴⁵; b = 3³⁶; c = 4²⁷; d = 5¹⁸
сравним а = 2⁴⁵ и c = 4²⁷
4²⁷ = 2⁵⁴
Понятно. что 2⁵⁴ > 2⁴⁵, значит, с > a
Сравним b = 3³⁶ и d = 5¹⁸
3³⁶ = 9¹⁸
Понятно. что 9¹⁸ > 5¹⁸, значит, b > d
Сравним b = 3³⁶ и c = 4²⁷
3²⁷· 3⁹ и 4²⁷
3 · 3⁻³ и 4
3⁻² и 4
1/9 < 4, значит, с > b и c - cамое большое число и з всех четырёх чисел
Сравним а = 2⁴⁵ и d = 5¹⁸
2¹⁸· 2²⁷ и 5¹⁸
2 · 2√2 и 5
4√2 и 5
5,66 > 5, значит, а > d и d - самое маленькое число из четырёх
Сравним а = 2⁴⁵ и b = 3³⁶
2³⁶· 2⁹ и 3³⁶
2 · ⁴√2 и 3
2 · 1,19 и 3
2,38 < 3, значит, а > b
Получили такой ряд: с > b > a > d
1001*x + 100*y + 10z = 25*z^2 + 10*z + 1
1001*x + 100*y - 1 = 25*z^2
Итак, 25*z^2 = 1001*x + 100*y - 1
Рассмотрим выражение (5*z + 1)^2, оно д.б. больше 1000, т.к. число четырёхзначное: (5*z + 1)^2 ≥ 1000, отсюда получаем, что
5*z + 1 ≥ 32 (корень из 1000 больше 31, но меньше 32).
Значит, z ≥ 31/5 или z ≥ 7 (зет целое, поэтому 6 исключаем в виду того, что оно д.б. больше 6,2) и z ≤ 9 (т.к. это цифра самая большая).
Пробуем подобрать.
z = 7; 25 * 7^2 = 1225 = 1001*x + 100*y - 1, или 1001*x + 100*y = 1226, что невозможно в целых числах.
z = 8; 25 * 8^2 = 1600 = 1001*x + 100*y - 1, или 1001*x + 100*y = 1601, что возможно при x = 1 и y = 6.
z = 9; 25 * 9^2 = 2025 = 1001*x + 100*y - 1, или 1001*x + 100*y = 2026, что невозможно в целых числах.
Итак, есть один вариант, где x = 1, y = 6, z = 8
Исходное четырёхзначное число было равно 1681.
ответ: z = 8