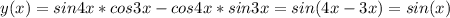
 есть
есть 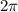
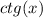 равен
равен 
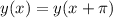
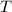 - искомый период, тогда
- искомый период, тогда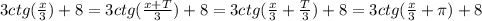
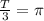

 относительно оси OX на 8 единиц вверх, также не влияя на период
относительно оси OX на 8 единиц вверх, также не влияя на период

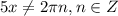
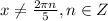
 - это симметричное относительно начала координат множество точек,
- это симметричное относительно начала координат множество точек, также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
решите систему уравнений методом подстановки общая скобка один пример сверху другой снизу 3x-y=-5. -5x+2y=1, т. е из одного уравнения выразить одну переменную и подставить во второе. Из двух уравнений проще выразить из первого у, т. к. коэффициент равен 1, получим
3x-y=-5
-5x+2y=1
Выражаем у из первого уравнения и ставим во второе
у=3х+5
-5х+2(3х+5)=1
Раскрываем скобки
у=3х+5
-5х+6х+10=1
Приводим подобные
у=3х+5
х+10=1
Отсюда
у=3(-9)+5
х=1-10
Или решением неравенства будет пара
у=-22
х=-9
Проверка
3(-9)-(-22)=-5
-5(-9)+2(-22)=1
Произведем вычисления
-27+22=-5
45-44=1
или
5=-5
1=1
Т. к. получили верное равенство, значит, решили правильно
ответ: х=-9 и у=-22 или (-9;-22)
Удачи!
Объяснение:
общее решение уравнения