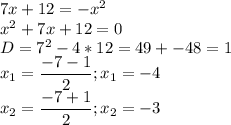
При х=3
Объяснение:
Определим, при каком значении х функция у = 4 * х - 1 принимает значение равное 11
Так как, y = 11, то подставим данное значение в функцию у = 4 * х - 1, и составим уравнение. То получаем уравнение в виде:
4 * x - 1 = 11;
Приведем уравнение к линейному виду и получим:
4 * x - 1 - 11 = 0;
4 * x - (1 + 11) = 0;
4 * x - 12 = 0;
Получили линейное уравнение в виде 4 * x - 12 = 0
Для того, чтобы решить уравнение, определим какие свойства имеет уравнение:
Уравнение является линейным, и записывается в виде a * x + b = 0, где a и b - любые числа;
При a = b = 0, уравнение имеет бесконечное множество решений;
Если a = 0, b ≠ 0, уравнение не имеет решения;
Если a ≠ 0, b = 0, уравнение имеет решение: x = 0;
Если, а и b - любые числа, кроме 0, то корень находится по следующей формуле x = - b/a.
Отсюда получаем, что a = 4, b = - 12, значит, уравнение имеет один корень.
x = - (- 12)/4;
x = 12/4;
x = 3 * 4/4;
Дробь 3 * 4/4 сокращаем на 4, тогда получим:
х = 3 * 1/1;
x = 3;
Получаем, что при х = 3 функция у = 4 * х - 1 принимает значение равное 11.
Перенесём -x² в левую сторону.
x² + 7x + 12 = 0
По теореме, обратной теореме Виета, получаем:
x₁ + x₂ = -7
x₁·x₂ = 12
x₁ = -3
x₂ = -4
Можно решить по-другому.
Выделим полный квадрат:
x² + 7x + 12 = 0
x² + 2·3,5x + 12,25 - 0,25 = 0
(x + 3,5)² - 0,5² = 0
(x + 3,5 - 0,5)(x + 3,5 + 0,5) = 0
Произведение множителей равно нулю, когда любой из множителей равен нулю:
x + 3,5 - 0,5 = 0 и x + 3,5 + 0,5 = 0
x = -3 и x = -4
И ещё один
Найдём дискриминант.
D = 49 - 4·12 = 1
x₁ = (-7 + 1)/2 = -3
x₂ = (-7 - 1)/2 = -4
ответ: x = -4; -3.