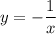и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
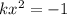и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
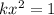и при k<0 это уравнение решений не имеет.
, имеем
Для вычисления понадобятся следующие определения и формулы.
arcsin b = α
Арксинусом числа b∈[-1; 1] называется угол α такой, что
sin α = b и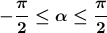 
.
arcsin (sin α) = α, если ![\boldsymbol{\alpha \in \Big[-\dfrac{\pi }{2}; \dfrac{\pi }{2}}\Big]](/tpl/images/0315/2594/4cc60.png)
sin (arcsin b) = b, где b∈[-1; 1]
cos (arcsin b) ≥ 0 и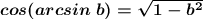 
, b∈[-1; 1]
sin (2α) = 2 sin α · cos α
=====================================================
sin (2arcsin 0,75) = 2 · sin(arcsin 0,75) · cos (arcsin 0,75)
0,75∈[-1; 1] ⇒ sin(arcsin 0,75) = 0,75 = 3/4
===================================================
===================================================
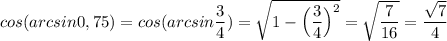
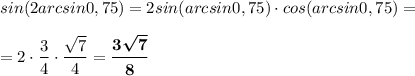
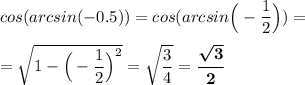
arcsin (sin2)
Так как 2 > π/2 ≈ 1,57, то есть 2∉[-π/2; π/2] , то нельзя сразу воспользоваться формулой arcsin (sin α) = α. Нужно преобразовать выражение с формул приведения.
arcsin (sin 2) = arcsin (sin (π - 2)) = π - 2
После преобразования угол (π - 2) ≈1,14 ∈ [-π/2; π/2]
y=11x+13, и y= -2x^2 + 3x + 5.
11x + 13 = -2x^2 + 3x +5,
2x^2 + x*(11-3) + 13-5 = 0;
2x^2 + 8x + 8 = 0;
x^2 + 4x + 4 = 0;
x^2 + 2x*2 + 2^2 = 0;
(x+2)^2 = 0;
x+2 = 0;
x= -2.
Во-вторых, если данные графики функций касаются, то в точке касания будет наблюдаться совпадение тангенса угла наклона касательных, то есть касательные к графикам функций в искомой точке совпадут, что значит совпадут значения производных функций в искомой точке.
y1' = (11x+13)' = 11,
y2' = (-2x^2 + 3x + 5)' = (-2)*2x + 3,
11 = (-2)*2x + 3;
11 = -4x + 3;
4x = 3-11 = -8;
x = -8/4 = -2.
ответ. x=-2.