![y=\begin{cases} & \text{ } 3x+7,\,\,\,\, x\ \textless \ -1 \\ & \text{ } 2|x-1|,\,\,\,\, x \in [-1;2] \\ & \text{ } -2x+6,\,\,\,\, x\ \textgreater \ 2 \end{cases}](/tpl/images/0777/5020/af216.png)
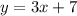- прямая, которая проходит через точки (0;7), (-7/3;0).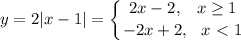
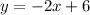- прямая, которая проходит через точки (0;6), (3;0).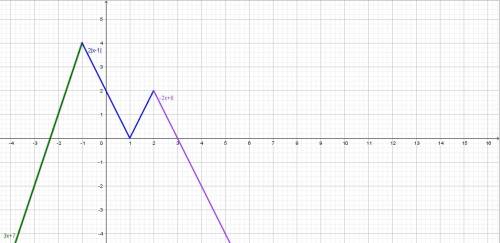
Объяснение:
27.
а) a₁=7, aₙ₊₁=aₙ+8
a₂=a₁₊₁=a₁+8=7+8=15
a₃=a₂₊₁=a₂+8=15+8=23
a₄=a₃₊₁=a₃+8=23+8=31
a₅=a₄₊₁=a₄+8=31+8=39
a₆=a₅₊₁=a₅+8=39+8=47
7; 15; 23; 31; 39; 47
б) b₁=1/2, bₙ₊₁=3bₙ
b₂=b₁₊₁=3b₁=3·1/2=3/2=1 1/2
b₃=b₂₊₁=3b₂=3·3/2=9/2=4 1/2
b₄=b₃₊₁=3b₃=3·9/2=27/2=13 1/2
b₅=b₄₊₁=3b₄=3·27/2=81/2=40 1/2
b₆=b₅₊₁=3b₅=3·81/2=243/2=121 1/2
1/2; 1 1/2; 4 1/2; 13 1/2; 40 1/2; 121 1/2
в) c₁=-2; c₂=1; cₙ₊₁=cₙ₋₁+cₙ
c₃=c₂₊₁=c₂₋₁+c₂=-2+1=-1
c₄=c₃₊₁=c₃₋₁+c₃=1-1=0
c₅=c₄₊₁=c₄₋₁+c₄=-1+0=-1
c₆=c₅₊₁=c₅₋₁+c₅=0-1=-1
-2; 1; -1; 0; -1; -1
г) d₁=1; d₂=2; dₙ₊₂=dₙ·dₙ₊₁
d₃=d₁₊₂=d₁·d₁₊₁=1·2=2
d₄=d₂₊₂=d₂·d₂₊₁=2·2=4
d₅=d₃₊₂=d₃·d₃₊₁=2·4=8
d₆=d₄₊₂=d₄·d₄₊₁=4·8=32
1; 2; 2; 4; 8; 32
Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
\[a{x^2} + bx = 0\]
Общий множитель x выносим за скобки:
\[x \cdot (ax + b) = 0\]
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
\[x = 0;ax + b = 0\]
Второе уравнение — линейное. Решаем его:
\[ax = - b\_\_\_\left| {:a} \right.\]
\[x = - \frac{b}{a}\]
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
\[1){x^2} + 18x = 0\]
Общий множитель x выносим за скобки:
\[x \cdot (x + 18) = 0\]
ДОЛЖНО БЫТЬ ПРАВИЛЬНО
