Объяснение:
6a^2-6a+2=0, 3a^2-3a+1=0, D=9-12=-3<0, нет решения
5(x^2+4x+4)+6x+14=0, 5x^2+20x+20+6x+14=0, 5x^2+26x+34=0,
D=676-4*5*34=676-680=-4<0, нет решения
подставим 4а во второе уравнение системы. получим 4ху=2х²+2у²-2, упростим
-2ху+х²+у²=1; (х-у)²-1=0; (х-у-1)*(х-у+1)=0; 1)х=у+1 или 2)х=у-1 получили две прямые.
Если х=у+1,то 4у*(у+1)+2=а; 4у²+4у+2=а; (2у+1)²=а-1; Если а=1 ,то получим один корень, если а>1, то два корня. Если а<1, то корней нет.
Если рассмотреть первое уравнение, то при каждом a ≠ 0 — уравнение окружности c центром (0, 0) и радиусом а√2, тогда система при а=0 имеет единственное решение и поэтому не удовлетворяет условию задачи. При а≤0 уравнение не имеет смысла.
используем теперь результат выше и уточним ответ на задачу.
Если х=у+1, то у²+у²+2у+1=2а,у²+у+1/2=а; (у+1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
Если х=у-1, то у²+у²-2у+1=2а,у²-у+1/2=а; (у-1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
40
Объяснение:
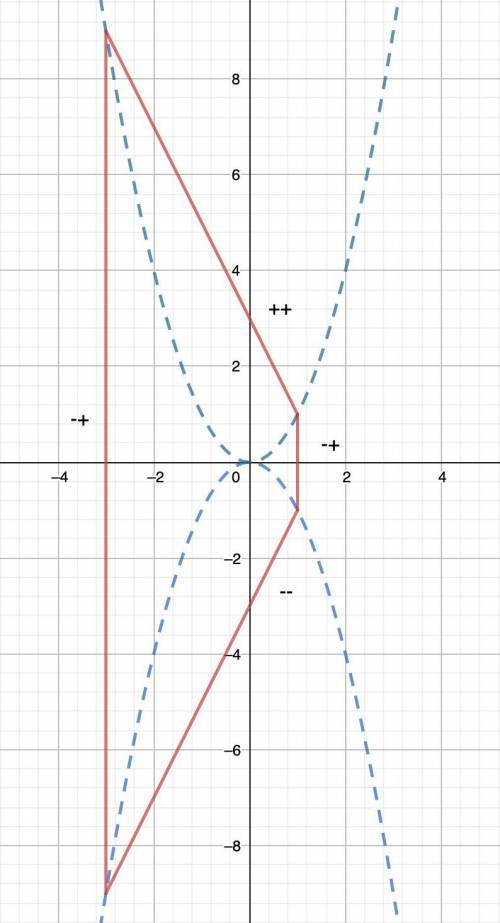
Модули принимают значение 0, когда y = x² и y = -x². Начертим графики этих функций (синие, пунктирные). Они делят плоскость на 4 области. Рассмотрим, как раскрываются модули: "внутри" верхней параболы оба модуля раскрываются с плюсом (убеждаемся подстановкой точки x = 0, y = 1, оба подмодульных выражения положительны, обозначим как ++), "внутри" нижней — оба с минусом (подставляем x = 0, y = -1, обозначим как --), "снаружи" обеих парабол — первый с минусом, второй с плюсом (подставляем x = ±1, y = 0, обозначим как -+).
Рассмотрим разные случаи раскрытия модулей:
++: 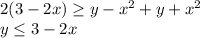
y = 3 - 2x — прямая, заключённая внутри верхней параболы. По неравенству нам подходит всё, что ниже этой прямой. Она пересекает параболу y = x² при x² = 3 - 2x ⇔ x² + 2x - 3 = 0 ⇔ x = -3; 1.
--: 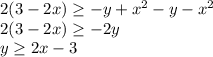
y = 2x - 3 — прямая, заключённая внутри нижней параболы. По неравенству подходит всё, что выше этой прямой. Она пересекает параболу y = -x² при -x² = 2x - 3 ⇔ x² + 2x - 3 = 0 ⇔ x = -3; 1.
-+: 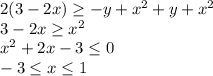
x = -3; 1 — это две вертикальные прямые, заключённые между параболами (в области -+). По неравенству подходит всё, что между ними. Они пересекаются с параболами в тех же точках, что и прямые.
Красным обозначим полученные отрезки. Из предыдущих рассуждений получаем, что нам подходит всё, что внутри красной фигуры. Эта фигура — трапеция, так как её основания (вертикальные прямые x = -3; 1) параллельны и не равны (длина первого отрезка — 2·(-3)² = 18, длина второго — 2·1² = 2, умножаем на 2 в силу симметрии графиков y = x² и y = -x² относительно Ox). Высота — расстояние между этими прямыми, то есть 1 - (-3) = 4. Площадь трапеции равна 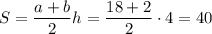
Надеюсь правильно решил.
6а^2+2=6a | :2
3a^2+1=3a
3a^2-3a+1=0
D=(-3)^2-4*3*1=9-12=-3 (корней нет т.к D<0)
5(х+2)^2=-6x-14
5*(x^2+4x+4)=-6x-14
5x^2+20x+20=-6x-14
5x^2+2x+20+6+14=0
5x^2+9x+34=0
D=8^2-4*5*34=64-680=-16 (корней нет т.к D<0)
я не знаю, что за фигня но почему-то везде нет корней и D<3.
Объяснение: