x = 4; y = 5.
Объяснение:
1) Метод подстановки
решим нижнее уравнение относительно x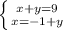
зная значение x из нижнего уравнения, подставим значение x в верхнее уравнение 
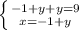решаем верхнее уравнение как обычное уравнение 
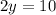y = 5;Дальше решаем нижнее уравнение как обычное уравнение, зная, что y = 5 
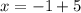;x = 4.2) Метод исключения переменной
сложим два уравнения вместе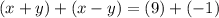
;решим это уравнение как обычное уравнение 
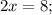;x = 4.Подставим значение x в уравнение x+y=9 
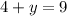;y = 5.3) Метод сравнения
перенесем все y в правые части выражений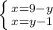
;зная, что и 9-y и y-1 равны x - сравним их 
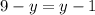;решим это уравнение как обычное уравнение 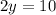;y = 5подставляем значение y в выражение x = y-1 
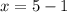;x = 4.Если мой ответ этого заслуживает, отметь его как лучший . Это очень важно для меня
возьмем собственную скорость реки за Х, тогда скорость по течению = Х + 1, а скорость против течения = Х - 1
найдем время по течению и против течения: время по течению = путь / скорость = 63/(х+1)
время против течения = 63/(х-1)
известно, что на обратный путь лодка потратила на 2 часа меньше. составляем уравнение:
63/(х+1) + 2 = 63/(х-1)
63х - 63 + 2х^2 -2=63х + 63
2х^2 - 128=0
х^2 = 64
х=8 х=-8 - не удовлетворяет условию, значит ответ: х=8
вот все то же самое только в место 63, 96 поставь и решай!!
Задание. Найти площадь прямоугольного треугольника , если известно, что длины его катетов равны 3 см и 4 см.
Решение. Искомая площадь равна половине произведения катетов, то есть
S/_ авс= 3*4/2= 12/2= 6 (см2)
ответ. S/_ авс 6 (см2)