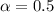- вероятность победы
Иван и Алексей сыграют друг с другом в 1 туре, если так будет определено жеребьевкой.
Рассмотрим возможных соперников Ивана. Их 15 человек. Поэтому, вероятность того, что по результатам жеребьевки 1 тура Иван будет играть именно с Алексеем равна:
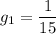
Таким образом, вероятность сыграть Ивану и Алексею в 1 туре между собой равна:
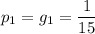
Если Иван и Алексей не сыграли между собой в 1 туре, то возможно они сыграют между собой во 2 туре. Но для этого каждому из них необходимо как минимум выиграть в 1 туре.
Вероятность того, что и Иван и Алексей окажутся во 2 туре, равна:
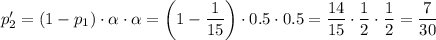
Во 2 туре играет 8 человек, то есть 7 возможных соперников для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:
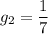
Значит, играть Иван и Алексей между собой во 2 туре будут с вероятностью:
Если Иван и Алексей не играли между собой во 2 туре, то они имеют шансы выйти в 3 тур. Это произойдет с вероятностью:
В 3 туре играет 4 человека, то есть 3 возможных соперника для каждого. По результатам жеребьевки 2 тура Иван будет играть с Алексеем с вероятностью:
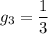
Значит, Иван и Алексей сыграют между собой в 3 туре с вероятностью:
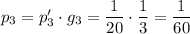
Вероятность выхода Ивана и Алексея в 4 тур:
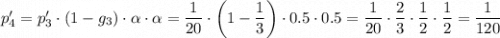
Если Иван и Алексей вышли в 4 тур, то есть в финал, то они, конечно, сыграют друг с другом:
Итоговая вероятность сыграть Ивану и Алексея друг с другом в каком-либо туре равна:
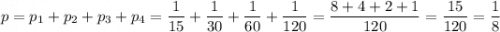
ответ: 1/8
Задано систему уравнений
{ ax² +3ax +4^(1+√y) =8 ; x+2*4^y = 1 где
x, y - переменные, а - произвольная постоянная . ( параметр ) .
1. Решите систему, если а = 0.
2. Определите все решения заданной системы в зависимости от значений а.
ответ 1 : если а = 0 , → ( - 3 , 0,25) . ,
ответ 2 :
одно решение: если а = -2/3 → ( - 3 , 0,25) ,
два решения: если а ≠ 0 и а ≠ -2/3
(x₁ ; y₁ ) → ( - 3 , 0,25) и (x₂ ; y₂ ) ⇒ (2/a ; 0,25( log₂ ( (a -2)/ 2a ) )²
Объяснение: ОДЗ : y ≥ 0
{ ax² +3ax +4^(1+√y) =8 ; x+2*4^y = 1. ⇔
{ ax² +3ax +4^(1+√y) =8 ; 2x+4^(1+√y) = 2.
{ ax² +3ax + 4^(1+√y) =8 ; 4^(1+√y) = 2 -2x . ⇒
ax² +3ax +2 -2x = 8
ax² -(2 -3a)x - 6 = 0
1. Если а = 0 (линейное уравнение)
0 -2x - 6=0 ⇒ x = - 3 ;
4^(y) = (1 -x)/2 ⇒ 2^(2√y) = 2¹ ⇔2√y) = 1 ⇔
√y = 0,5 ⇒ y = 0,25 ответ 1 : (-3 ; 0,25)
2. Если а ≠ 0 имеем квадратное уравнение
ax² - (2-3a)x -6 = 0 дискриминант которого
D = ( 2 -3a )² - 4*1(-6) = ( 2 +3a )² ≥ 0 , следовательно данное кв. уравнение для любого значения параметра a имеет решение.
2.а одно решение , если D = 0 , т.е. при а = -2/3
x₀ = (2-3a)/2a = 1/a - 3/2 = - 3/2 -3/2 = - 3 ⇒ y₀ = 0,25
два решения, если D ≠ 0 , т.е. при { а ≠ -2/3 ; а ≠ 0 }
x₁ =( 2 -3a) - (2 +3a ) ) / 2a = -3 ⇒ y₁ = 0,25 ;
- - - - - - - - - - - -
x₂ = ( 2 -3a) + (2 +3a ) ) / 2 a = 2/a ;
4^(√y₂) = (1 -x₂) /2 ⇔ 2^(2√y₂) = (a -2)/2a
* * * (a- 2)/2a >0 ⇒ a ∈ (- ∞ ;0) ∪ (2; ∞) * * *
2√y₂ = log₂ ( (a -2)/2a ) ⇔ √y₂ =0,5( log₂ ( (a -2)/2a )
имеет решения , если log₂ ( (a -2)/ 2a ) ≥ 0
(a -2)/ 2a ) ≥ 1
(a - 2) / 2a) - 1 ≥ 0
(a - 2 - 2a) /2a ≥ 0
(a + 2)/ a ≤ 0
+ + + + + + [ -2] - - - - - (0) + + + + + + +
a ∈ [ -2 ; 0 ) , учитывая а ≠ -2/3
получается a ∈ [ -2 ; -2/3 ) ∪ (-2/3 ; 0 )
y₂=0,25( log₂ ( (a -2)/ 2a ) )²
* * * 3 раза повторяется решения ( - 3 , 0,25) * * *
b^2(a+1)-a^2(b+1) = ab² + b² - a²b - a² = ab² - a²b + b² - a² =
= ab(b - a) + (b + a)(b - a) = (b - a)(ab + b + a)