Моторний човен подолав 36 км проти течії повернувся назад за 5 год. знайдіть власну швидкість човна якщо швидкість течії 3 км/год

👇

Ответ:

qwetdfgdsa

29.07.2022

Пусть собственная скорость будет х км/ч, тогда скорость по течению равна (x+3) км/ч, а против течения - (х-3) км/ч. Время по течению - 36/(х+3), а против течения - 36/(х-3) ч. На весь путь лодка затратила 5 часов.

Составим уравнение

$\displaystyle \frac{36}{x-3}+ \frac{36}{x+3}=5\,\,\, |\cdot(x^2-9)\ne0\\ \\ 36(x+3)+36(x-3)=5(x^2-9)\\ \\ 36x+36x=5x^2-45\\ \\ 5x^2-72x-45=0\\ \\ D=5184+900=6084\\ \\ x_1=15$

x_2=-0.6

- противоречит условию

ответ: 15 км/ч.

4,6(43 оценок)

Открыть все ответы

Ответ:

denvolk00

29.07.2022

Определить промежутки монотонности функции, не используя производную функции.

y = (x² - x - 20)² - 18

=================================

Область определения функции D (y) = R

y = (x² - x - 20)² - 18

Квадратичная функция в квадратичной функции

y = f(z); z = g(x)

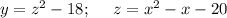
$y = z^2-18;\ \ \ \ z=x^2-x-20$

Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.

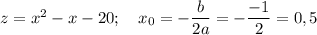$z=x^2-x-20;\ \ \ x_0=-\dfrac b{2a}=-\dfrac {-1}2=0,5$ - координата вершины

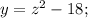y = z^2-18; z = 0 - координата вершины параболы

$x^2-x-20=0\\(x-5)(x+4)=0$

x₁ = -4; x₂ = 5 - координаты вершин параболы

Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.

x₁ = -4; x₀ = 0,5; x₂ = 5

x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)

x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)

x ∈ [0,5; 5] - функция убывает : y(1) > y(2)

x ∈ [5; +∞) - функция возрастает : y(5) < y(6)

4,7(51 оценок)

Ответ:

Vanilingus

29.07.2022

Для начала найдём, при каких значениях m корни вообще есть. Для этого D≥0.
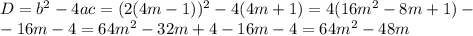
$D = b^2-4ac=(2(4m-1))^2-4(4m+1)=4(16m^2-8m+1)- \\ -16m-4=64m^2-32m+4-16m-4=64m^2-48m$
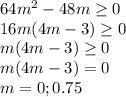
$64m^2-48m \geq 0 \\ 16m(4m-3) \geq 0 \\ m(4m-3) \geq 0 \\ m(4m-3)=0 \\ m=0; 0.75$
Решая методом интервалов, получаем: $m\in(-\infty; 0]\cup[0.75; +\infty)$ . Это наша ОДЗ.

По теореме Виета
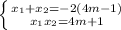
$\left \{ {{x_{1}+x_{2}=-2(4m-1)} \atop {x_{1}x_{2}=4m+1}} \right.$
Попробуем подогнать сумму квадратов корней под теорему Виета:
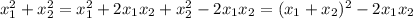
$x_{1}^{2}+x_{2}^{2}=x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2}-2x_{1}x_{2}=(x_{1}+x_{2})^2-2x_{1}x_{2}$
Подставляем:
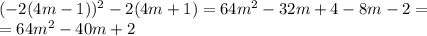
$(-2(4m-1))^2-2(4m+1)=64m^2-32m+4-8m-2= \\ =64m^2-40m+2$
Это парабола, ветви направлены вверх, значит, её точка минимума находится в её вершине. Если она принадлежит ОДЗ, то это и будет ответом, если нет - то либо 0, либо 0.75 (концы отрезков ОДЗ).
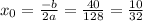
$x_{0}= \frac{-b}{2a} = \frac{40}{128} = \frac{10}{32}$
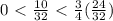$0\ \textless \ \frac{10}{32} \ \textless \ \frac{3}{4} ( \frac{24}{32} )$ - не подходит. Проверяем концы отрезков:
При m = 0 сумма квадратов корней будет равна 2.
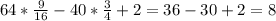При m = 0.75 сумма квадратов корней будет равна $64 * \frac{9}{16} - 40 * \frac{3}{4} + 2 = 36 - 30 + 2 = 8$ . Подходит первый вариант.

ответ: при m = 0.

4,7(57 оценок)

Это интересно:

Кулинария-и-гостеприимство

02.04.2023

Купить семена льна: Советы по выбору и покупке...

Компьютеры-и-электроника

27.10.2022

5 простых способов избежать травли в интернете...

Образование-и-коммуникации

21.03.2023

10 способов развить способность к обучению...

Финансы-и-бизнес