Речь идёт о площадях подобных треугольников.
Их площади относятся как квадраты коэффициентов подобия.
Размеры светлого треугольника: основание равно 1-(-1) = 2, высота равна 2-0 = 2. Его площадь S1 = (1/2)2*2 = 2 кв.ед.
Треугольник, состоящий из светлого и закрашенной фигуры, имеет высоту, равную 2-(-1) = 3.
То, что они подобны видно по рисунку - основания треугольников параллельны. То есть они попадают под следствие: прямая, пересекающая треугольник и параллельная стороне треугольника, отсекает от этого треугольника подобный треугольник.
Коэффициент подобия определяем по соотношению высот и он равен 3/2.
Площадь большего треугольника S2 = S1*(3/2)² = 2*(9/4) = 9/2 кв.ед.
ответ: S3 = S2 - S1 = (9/2) - 2 = 5/2 кв.ед.
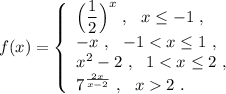
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
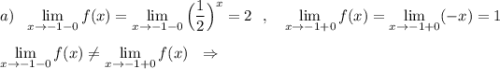
При х= -1 функция имеет разрыв 1 рода .

При х=1 функция непрерывна.
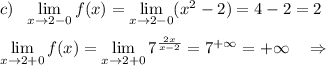
При х=5 функция имеет разрыв 2 рода .
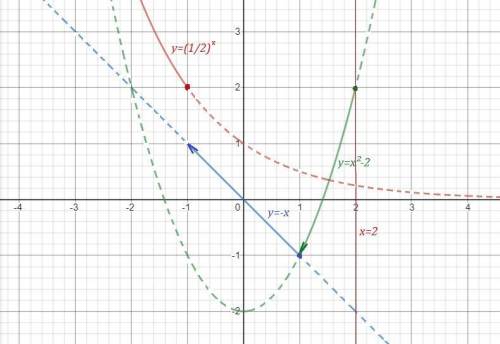
График функции нарисован сплошными линиями.
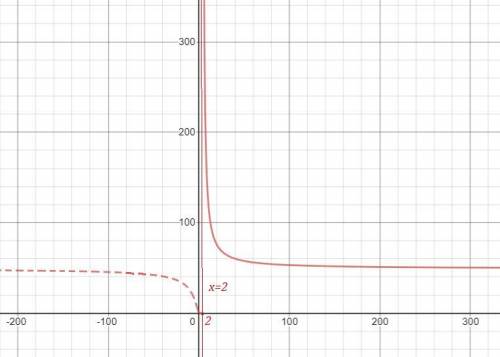
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
второй икс равен 4
-1<0
4>0