Пусть скорость третьего атомобиля равна х км\час, за час первый автомобиль км, второй разница скоростей третьего и первого автомобиля равна (x-80) км\час, третий автомобиль догнал первый за 80/(x-80) час. За время от начала движения второй автомобиль проехал (80/(x-80)+1)*100=8000/(x-80)+100 км, расстояние от второго автомобиля до третьего равно 8000/(x-80)+100 -80/(x-80)*x км, разница скоростей третьего и второго автомобилей равна (х-100) км\час, по условию задачи третйи автомобиль догонит третий за (составляем уравненение)
(8000/(x-80)+100 -80х/(x-80)) :(x-100)=3
8000+100(х-80)-80х=3(x-80)(x-100)
8000+100x-8000-80x=3(x^2-180x+8000)
20x=3x^2-540x+24000
3x^2-560x+24000=0
D=25 600=160^2
x1=(560-160)/(2*3)<80 - не подходит условию задачи (скорость третьего автомобиля не может быть меньшей за скорость второго , меньшей за скорость первого)
x2=(560+160)/(2*3)=120
х=120
ответ:120 км\час
Четыре числа образуют геометрическую прогрессию. Если к ним прибавить соответственно 6, 12, 14 и 8, тогда получим четыре числа, которые образуют арифметическую прогрессию. Найди числа, которые образуют геометрическую прогрессию.
знаменатель геометрической прогрессии: q= 2
члены геометрической прогрессии :
b1= 4
b2=8
b3= 16
b4=32
Решение
b₁; b₁·q; b₁·q²; b₁·q³ геометрическая прогрессия
тогда
b₁+6; b₁·q+12; b₁·q; b₁·q³ арифметическая прогрессия
по характеристическому свойству арифметической прогрессии
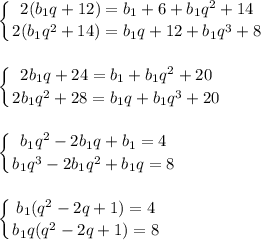
q ≠ 1
разделим второе уравнение на первое
q = 2
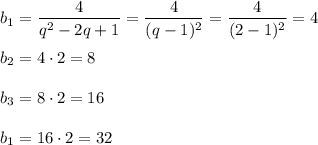
3х + у = 9
Решение методом сложения
- у + Х = 0
3х - у + у + Х = 9
4х = 9
Х = 2,25
У - 2,25 = 0
у = 2,25
ответ ( 2,25 ; 2,25 )