1.D=1-40=-39 D<0 корней нет
a)D=121+198=289
x1=-1, x2=12
b)D=25-16=9
x1=-2, x2=-1/2
в)x^4=0, т.е.х1=0
-13х^2+36=0
13x^2-36=0
x^2=36/13
x2=-6/корень из 3
х3=6/корень из 3
y = 4x - x² - Квадратичная функция, график - парабола, ветви направлены вниз ( a = -1). Максимальное значение принимает в вершине, минимальное значение не имеет, снизу не ограничена.
a) Координаты вершины параболы
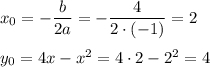
x₀=2 ∈ [0; 3] ⇒ x₀=2 - точка максимума функции попадает в заданный интервал, наибольшее значение функции y₀ = 4.
Значения функции на границах интервала
x = 0; y = 4·0 - 0² = 0
x = 3; y = 4·3 - 3² = 3
Наименьшее значение y = 0 при x = 0.
б) x∈(-∞; 2] - функция возрастает
x∈[2; +∞) - функция убывает
в) 4x - x² < 0 ⇔ x (4 - x) < 0
Метод интервалов : x₁ = 0; x₂ = 4
------------ (0) +++++++++ (4) -----------> x
x∈(-∞; 0) ∪ (4; +∞)
1)корней нет, т.к дискриминат меьше ноля
2)2x2+5x+2=0
D=3
x1=-1/4
x2= -1
3)x2=y
y-13y+36=0
D=5
y1= 9
y2=4
x2=9 x2=4
x=3;-3 ч=2;-2