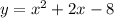
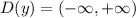
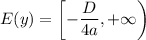 - где D дискриминант.
- где D дискриминант.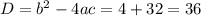
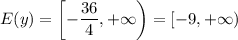
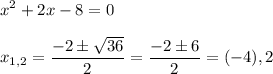
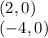



![(-\infty,-1]](/tpl/images/0467/5865/91666.png)
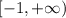

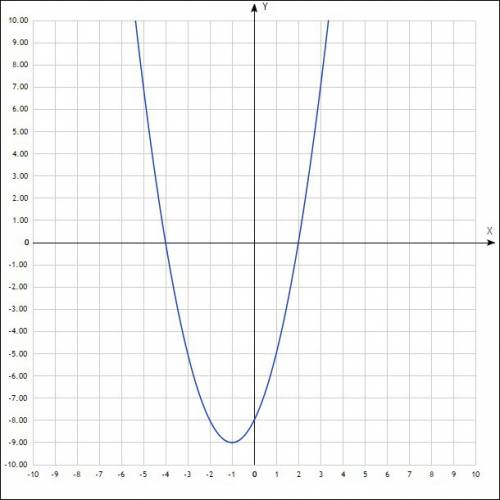
"Дана функция y=x2−4. Построй график функции y=x2−4.
a) Координаты вершины параболы: ( ; )
(в пунктах б), в) и г) вместо −∞, пиши «−Б»; вместо +∞, пиши «+Б»).
б) При каких значениях аргумента значения функции отрицательны?
( ; ). в) При каких значениях аргумента функция возрастает? [ ; ).
г) При каких значениях аргумента функция убывает? ( ; ]
(Сравни свой график с представленным в шагах решения).
Объяснение:
a) Координаты вершины параболы: х₀=0/2=0 , у₀=0-4=-4 ; (0 ;-4 ) .
б) у<0 при х²-4<0
-------(+)------(-2)--------(-)--------(2)------(+) ,при х∈ (-2;2)
в) Функция возрастает при х≥0.
г) Функция убывает при х≤0.
Для k = 2 он положил 1 карточку на место 2, а 2 карточку на место 1.
Теперь 1 карточка лежит на месте 2.
Для k = 3 он карточку 2 положил с места 1 на место 3, карточку 1 оставил на месте 2, а карточку 3 положил на место 1.
Теперь 1 карточка лежит на месте 2.
Для k = 4 он положил карточку 3 с места 1 на место 4, карточку 1 с места 2 на место 3, карточку 2 с места 3 на место 2, карточку 4 на место 1.
Теперь 1 карточка лежит на месте 3.
Для k = 5 карточка 1 останется на месте 3 - посередине ряда.
Для k = 6 карточка 1 попадет на место 4 - следующее после середины..
Для любого нечетного k карточка 1 будет всегда в середине ряда.
Для любого четного k карточка 1 будет на 1 правее середины ряда.
Для k = 199 карточка 1 окажется на 200/2 = 100 месте.
Для k = 200 карточка 1 окажется на 101 месте.