x3+x−2=0
x3+x−2=0Ищем первый корень через делители числа -2.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.
x3+x−2=0Ищем первый корень через делители числа -2.D=-2;-1;1;2Очевидно, что корень будет x=1Далее делим в столбик начальное выражение на корень уравнения (x-1)Получаем результат x^{2}+x+2x2+x+2 .Приравниваем его к нулю, видим, что корней нет, так как дискриминат отрицательный.Следовательно, ответ: x=1
Задача: Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.
Рішення: Нехай х км/год — швидкість човна в стоячій воді, тоді швидкість човна за течією — х+3 км/год, а проти течії — х-3 км/год. Човен пройшов 8 км за течією 8/(х+3) год, а проти течії — 5/(х-3) год. Весь шлях човен пройшов за 1 год. Складемо і вирішимо рівняння.
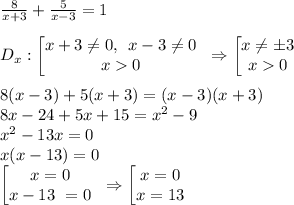
Відповідь: Швидкість човна у стоячій воді дорівню 13 км/год.
5,08=29/5
-2,2=-22/10