Найти площадь криволинейной трапеции ограниченной прямыми x=a,x=b,осью 0x и графиком функций y=f(x)

Question

Алгебра: Найти площадь криволинейной трапеции ограниченной прямыми x=a,x=b,осью 0x и графиком функций y=f(x)

rayarybak · Accepted Answer

Задача: Моторний човен пройшов 8 км за течією річки і 5 км проти течії, затративши на весь шлях 1 год. Знайти швидкість човна у стоячій воді, якщо швидкість течії річки дорівнює 3 км/год.

Рішення: Нехай х км/год — швидкість човна в стоячій воді, тоді швидкість човна за течією — х+3 км/год, а проти течії — х-3 км/год. Човен пройшов 8 км за течією 8/(х+3) год, а проти течії — 5/(х-3) год. Весь шлях човен пройшов за 1 год. Складемо і вирішимо рівняння.

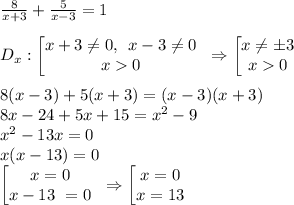
$\frac{8}{x+3} +\frac{5}{x-3}=1\\\\D_x: \begin {bmatrix} x+3\neq 0, \:\: x-3\neq 0 \\x0\end. \Rightarrow \begin {bmatrix} x\neq \pm 3 \\x0 \end.\\\\8(x-3)+5(x+3)=(x-3)(x+3)\\8x-24+5x+15 = x^2-9\\x^2-13x=0\\x(x-13)=0\\\begin {bmatrix} x=0 \\ x-13\ = 0 \end. \Rightarrow \begin {bmatrix} x = 0 \\ x = 13 \end.$

Відповідь: Швидкість човна у стоячій воді дорівню 13 км/год.

MOGZ ответил