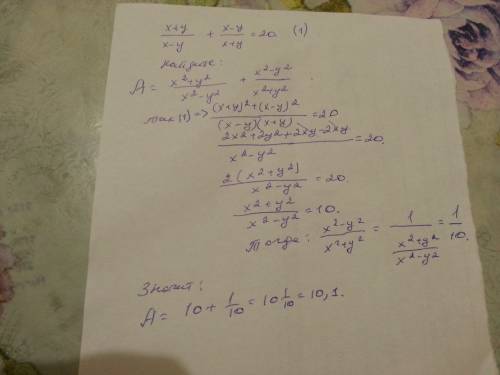
d = 8/5
Объяснение:
5x^2-6x+d=0
Пусть
x_1 = 2x_2, где
x_1 - первый корень квадратного уравнения
x_2 - второй корень квадратного уравнения,
тогда по теореме Виета (дла случая а≠1) запишем систему:
(x_2)*(2x_2)= d/5;
x_2+2x_2= 6/5;
решаем:
2*(x_2)^2=d/5;
3x_2=6/5;
далее:
2(x_2)^2=d/5;
x_2=6/(5*3) = 2/5;
подставим в первое уравнение
2*((2/5)^2)=d/5;
d/5= 2*4/25=8/25;
d/5=8/25;
d=40/25=8/5
Проверка:
5x^2-6x+8/5=0
D=6^2-4*5*8/5=36-32=4;
x_12=1/10*(6±√(4));
x_1= 8/10; x_2=4/10
x_1/x_2=(8/10)/(4/10)=2 как в условии!
x_1*x_2=8/10*4/10=32/100=8/25=d/5 - правильно
x_1+x_2=4/10+8/10=12/10=6/5=-(-6)/5 - верно!
1 график функций,
y = x^2 - 6x + 8
D = 36 - 4 * 8 = 4
x1, x2 = (6+-2)/2
x1 = 4
x2 = 2
Это нули функции.
График:
Ветки параболы направлены вверх, нули ты знаешь, x вершины = -b/2a = 6/2 = 3
Чтобы найти y вершины, подставь x=3 в выражение.
2 график функции
y= (x-4)^{2} - квадратичная функция, графиком которой является парабола.ветви параболы направлены вверх.парабола получена параллельным переносом по оси Ox графика функции y= x^{2} на 4 единицы вправо Проходит через точки (0,16) , (8,16) , (2,4) , (6, 4)