1)
По теореме Виета для уравнения 4х²-6х-1 :
х1+х2 = 1.5
х1*х2 = -0.25
2)
По теореме Виета для нового уравнения :
В = -(у1+у2) = -((2/х1³)-1 +(2/х2³)-1) = 578
С = -(у1*у2) = ((2/х1³)-1)*((2/х2³)-1) = 321
Уравнение : y²+578y+321 = 0
ответ : у²+578у+321 = 0
P.S если интересно как я из -((2/х1³)-1 +(2/х2³)-1) получил 578, то я сейчас примерно покажу (для удобства пусть х1 будет х, а х2 будет у) :
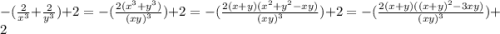
Ну и уже по теореме Виета (х+у = 1.5, х*у = -0.25) я подставил значения и решил, с умножением там примерно тоже самое)
а) b^3(b^2-8b-3)
б) 5x-8cx - 5y + 8cx = x( 5-8c ) - y( 5-8c ) = (x-y) ( 5-8c )
в) x^2 - 5x - y^2 + 5y = x( x-5 ) - y( у-5 ) - вот тут у меня вопрос - дальше не раскладывается, я даже проверил свои вычисления через одноимённый калькулятор, но, увы, он выдаёт такой же результат. Вы правильно переписали? Просто в данном случае дальше не раскладывается, а это весьма необычно.