I рабочий за 21 часов и II рабочий за 28 часов
Объяснение:
Объём задания примем за 1. Пусть I рабочий выполнить задание за х часов, и по условию, I рабочий выполнить задание на 7 часов быстрее чем II рабочий, то есть II рабочий выполнить задание за (х+7) часов.
Тогда производительность I рабочего за 1 час будет 1/х часть задания, а производительность II рабочего за 1 час будет 1/(х+7) часть задания. По условию оба рабочих работая вместе выполнили задание за 12 часов, то за 1 час они вместе выполнили 1/12 часть задания. Приравниваем данные за 1 час работы:
1/х + 1/(х+7) = 1/12 | ·12·x·(x+7)
12·(x+7) + 12·x = x·(x+7)
12·x+84+12·x=х²+7·x
х²–17·x–84=0
D= (–17)²–4·1·(–84) = 289+336 = 625 = 25²
х₁=(17+25)/2 = 42/2 = 21 часов время работы I рабочего
х₂=(17–25)/2 = –4<0 не подходит.
Тогда время работы II рабочего равна
21 + 7 = 28 часов.
Первое задание
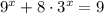
Сделаем замену 
, при этом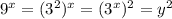 
. Получим уравнение:
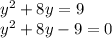
Тут по теореме Виета сразу видно, что первый корень равен единице. Тогда второй корень равен –9.
Вернёмся к исходной переменной:
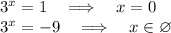
ответ: одно решение.
Второе задание
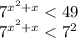
Основания степеней больше единицы, поэтому, переходя к неравенству показателйе, знак сохранится:
Приравняем левую часть выражения к нулю, решим через дискриминант и разложим на множители:
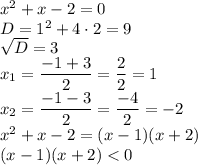
Применив метод интервалов, получим, что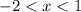 
. Поскольку неравенство строгое, имеем два целых решения: –1 и 0.
ответ: два решения.
Третье задание
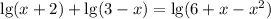
ОДЗ:
Или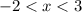 
Или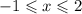 
(ведь речь о целых числах).
Теперь решим уравнение:
![\lg[(x+2)(3-x)]=\lg(6+x-x^2)\\(x+2)(3-x)=6+x-x^2\\3x+6-x^2-2x=6+x-x^2\\x+6-x^2=6+x-x^2\\0=0](/tpl/images/1010/8208/2a9fd.png)
Решений было бы бесконечное количество, если бы не ОДЗ: под него подпадают только числа –1, 0, 1, 2 (то есть четыре штуки).
ответ: четыре решения.
Четвёртое задание
ОДЗ:
Основание логарифма больше единицы, поэтому при переходе к неравенству выражений под логарифмом знак сохранится:
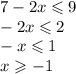
Решений было бы бесконечное количество, но с учётом ОДЗ получим: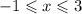 
. Здесь решениями будут числа –1, 0, 1, 2, 3.
ответ: пять решений.
Д= 20^2-4*7*(-3)= 400+84=484
Находим корни
х1= -20-22/14= -3
х2=-20+22/14= 1/7