
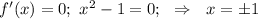
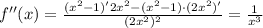

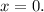



E(y)=[-4; 0]
Объяснение:
Нужно найти область значений, то есть E(y), функции у=х²-2·x-3 на промежутке [0;3].
Графиком функции является парабола, ветви которой направлены вверх. Определим абсциссу вершину параболы:
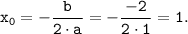
Так как x₀=1 ∈ [0; 3], то функция принимает наименьшее значение на этом промежутке:
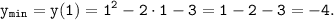
Далее, ветви параболы направлены вверх и поэтому наибольшее значение функция принимает на концах этого промежутка. Вычислим значение этой функции:
y(0)=0²-2·0-3= -3,
y(3)=3²-2·3-3= 0.
Отсюда, наибольшее значение функции
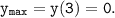
Значит, область значений функции на промежутке [0;3]: E(y)=[-4; 0].