ЗАДАЧА ПРО АВТОМОБИЛИ:10 АВТОМОБИЛЕЙ,потому что в неделе7 дней,а взрослых 8,значит в один день два автомобиля стоят и им нужна замена 8+2=10, ЗАДАЧА ПРО СОТРУДНИКОВ: Тот, кому не добавили рубль, относительно других сотрудников этот рубль теряет. Не доплачивать сотруднику с самой большой зарплатой до тех пор, пока его зарплата не сравняется с той, которая была самой маленькой (если сотрудников с наибольшей зарплатой - несколько, то выберем любого из них). Таким образом, наименьшую зарплату будут иметь, по крайней мере, двое сотрудников. Затем, снова выберем сотрудника с самой большой зарплатой и не будем ему доплачивать, пока его зарплата не сравняется с той, которая была самой маленькой, и получим не менее трех сотрудников с одинаковой зарплатой. Проделав такую операцию не более девяти раз, Ваня сможет уравнять все зарплаты.ЗАДАЧА ПРО ТЕЛЕФОН:
За один час разговора телефон разряжается на 100*1/6 = 50/3 %; за час покоя телефон разряжается на 100*1/210 = 10/21 %. Пусть х часов - половина времени в пути, тогда:
10/21 * х + 50/3 * х = 100 (разрядилось на 100%)
х * (10/21+50/3)=100
х*(10+350)/21=100
360х/21 = 100
х = 21*100/360
х = 5 целых 50/60 , т.е. 5 часов 50 минут
Поездка продолжалась 2* х, т.е. 11 ч 40 мин
1) После раскрытия скобок выражение принимает вид:
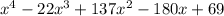 .
.
Эта функция имеет 2 минимума:
1. (0,8; 1,8)
2. (10,2; -36).
2) Запишем пропорцию - a/b = c/d a = b + 6 c = d + 5
(b + 6) / b = (d + 5) / d Отсюда 6d = 5b d = 5b / 6
По условию a^2 + b^2 + c^2 + d^2 = 793
Подставив значения, получим - (b + 6)^2 + b^2 + (d + 5)^2 + d^2 = 793.
После раскрытия скобок - 2b^2 + 12b + 2d^2 + 10d + 61 = 793/
Заменив d = 5b / 6 и приведя к общему знаменателю, получим
72b^2 + 432b + 50b^2 + 300b = 26352 или 122b^2 + 732b - 26352 = 0
Корни этого уравнения равны -18 и 12. Отрицательное значение отбрасываем - b = 12.
а =12 + 6 = 18 - это первый член пропорции
Два решения: (x1 = 12; y1 = 0); (x2 = 0; y2 = -3)
Эти решения - и есть координаты точек на осях: (12; 0), (0; -3)
График - прямая через эти две точки. Построить - как нечего делать.