2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
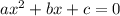
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
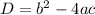
Формула корней:
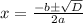
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
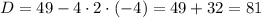
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
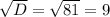
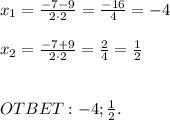
а) Так как знаменатели дробей равны, можем приравнять числители:
х² = 5х - 6
х² - 5х + 6 = 0, получили квадратное уравнение. Ищем корни.
х первое, второе = (5 + - √25-24) : 2
х первое = 6 : 2 = 3 х второе = 4 : 2 = 2
b) Здесь немного изменим знаменатель, чтобы приравнять числители:
5 - х = -х + 5 = - (х - 5)
Подставляем изменённый второй знаменатель во вторую дробь, она сразу становится со знаком -
Сейчас можно приравнять числители.
х² - 6х = -5
х² - 6х + 5 = 0 Получили квадратное уравнение, ищем корни:
х первое, второе = (6 + - √36 -20) : 2
х первое = 10 : 2 = 5 х второе = 2 : 2 = 1
c) Решено верно, проверено)
Объяснение:
\y - x = 7