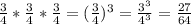
27/64
Объяснение:
Перемножь числитель: 3*3*3 =27
И знаменатель:4*4*4 =64
Итого:27/64

1) с использованием формул полного дискриминанта
7х² − х − 8 = 0
D = b² - 4ac = (-1)² - 4•7•(-8) = 1 + 224 = 225
x1 = (-b + √D)/(2a) = (1+15)/14 = 8/7 = 1 1/7!
x2 = (-b - √D)/(2a) = (1-15)/14 = - 14/14 = - 1.
ответ: - 1; 1 1/7.
2) с использованием формул половинного дискриминанта
3х² − 10х + 3 = 0
Если в уравнении ax2 + bx + c = 0
торой коэффициент b = 2k и является чётным, то дискриминант такого уравнения D1 = k2 − ac, а корни
х= (- k ± √D1)/a.
В нашем случае k = - 5,
D1 = 25 - 9 = 16
х= (5 ± √16)/3 = (5±4)/3
x1 = 1/3
x2 = 9/3 = 3.
ответ: 1/3; 3.
3) найти корни подбором, используя теорему, обратную теореме Виета
х² − 14х + 48 = 0
D = 196-192 > 0, уравнение имеет два корня.
Их произведение равно с/а = 48, а их сумма равна - b/a = 14.
{x1 • x2 = 48,
{x1 + x2 = 14.
такими числами являются 6 и 8. они и являются корнями уравнения.
ответ: 6; 8.