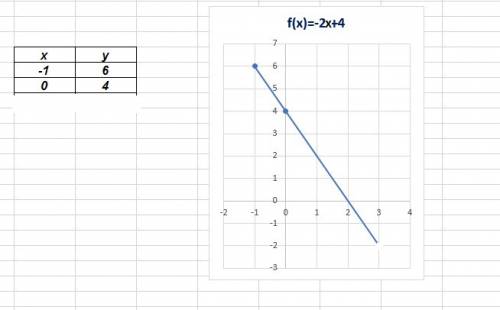
Для того, чтобы определить, проходит ли прямая через заданную точку, нужно координаты точки подставить в уравнение прямой.
у=-2х+4, х=0, у=4 => -2*0+4=0+4=4 - равенство верно, значит график проходит через точку (0;4)
у=-1/4х, х=0, у=4 => -1/4*0=4 - неверное равенство ( верно:-1/4*0=0), не проходит
х=4 - данная прямая проходит через точку х=4, параллельно оси 0У, уже в самой функции задано условие х=4, поэтому, через точку х=0, у=4, эта прямая не проходит
Для того, чтобы построить график функции у=-2х+4, нужно достаточно 2-х точек. Одна нам дана: (0;4), вторая точка, при, например, х=-1: у=-2*(-1)+4
у=2+4=6,
вторая точка - (-1;6)
Таблица и график во вложении
Разложите на множители выражение
(х+у)^2 - ( x^4- 2*x^2*y^2+ y^4 )=
=(х+у)^2 - ( x^2- y^2 )^2=
=(х+у)^2 - ( (x- y) (x+y) )^2=
=(х+у)^2 - (x- y)^2 (x+y)^2=
=(х+у)^2 (1 - (x- y)^2) =
=(х+у)^2 (1 - (x- y)) (1 +(x-y)) =
=(х+у)^2 (1 - x+ y) (1 +x-y)
Сократите дроби:
10а^2-6a+5ab-3b / 5a^2-8a+3=
=2a(5а-3)+b(5a-3) / 5a^2-5a-3a+3=
=(2a+b)(5a-3) / 5a(a-1)-3(a-1)=
=(2a+b)(5a-3) / (a-1)(5a-3)=
=(2a+b) / (a-1)
x^2-4x+1 / x^2-2(2+√3)x+(4+4√3+3)=
=x^2-4x+4-3 / x^2-2(2+√3)x+(2^2+4√3+√3^2)=
=(x-2)^2 - √3^2 / x^2-2(2+√3)x+(2+√3)^2=
=(x-2-√3) (x-2+√3) / ( x - (2+√3) )^2=
=(x-2-√3) (x-2+√3) / ( x- 2-√3)^2 =
=(x-2-√3) (x-2+√3) / ( x-2-√3) (x-2-√3)=
=(x-2+√3) / ( x-2-√3) или =(x+√3-2) / ( x-√3-2)