1. Формула которая была применена это, формула отрицательной степени дроби.
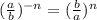 т.е эта формула говорит что дробь с отрицательной степенью "-n", равен дроби обратной с положительной степенью "n". Или своими словами дробь перевернули и степень лишилась минуса..
т.е эта формула говорит что дробь с отрицательной степенью "-n", равен дроби обратной с положительной степенью "n". Или своими словами дробь перевернули и степень лишилась минуса..
2. первую дробь переписали, дроби умножаются.
А на вторую дробь применили одно из свойств степени:
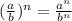
И в данном случае "а - числитель" это выражение поэтому степень распределяется на каждый член этого выражения: (a^(-2)×b^(3))³
И выполняется ещё одно свойство степени:
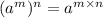
и тоже распределяется на каждый член выражения:
a^(-2×3)×b^(3×3)=a^(-6)×b^(9).
С числителем разобрались, переходим к знаменателю: 3, его также возводим в степень "3" по первому свойству которую я вам написал.
3. Чтобы умножить дробь на дробь, нужно: 1. Числитель первой дроби умножить на числитель второй дроби, и результат записать в числитель новой дроби. 2. Знаменатель первой дроби умножить на знаменатель второй дроби, и результат записать в знаменатель той же самой новой дроби. т.е:
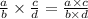
4. В числителе 9, и в знаменателе 27 успешно сокращаются на 9.
т.е и 9, и 27 делятся на 9.
в числителе остаётся. a^(-6)×b^(9).
В знаменателе "3" которая осталась от 27 после сокращения, умножается на 2, потому что от перемен мест множителей, произведение не меняется. получаем 6×a^(-3)×b(5).
5. Степени у оснований делителей сокращаются.
по свойству степени:
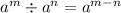
a^(-6)÷a^(-3)=a^(-6-(-3))=a^(-6+3)=a^(-3). (числитель)
b^(9)÷b^(4)=b^(9-4)=b^5; также у нас в знаменателе была "6". Поэтому знаменатель принимает такой вид: 6×b^(5)
дробь преобразовалась в такую:
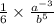
т.е a^(-3) делится на 6b^(5).
Чтобы поделить что-то на дробь, нужно: это "что-то" умножить на дробь обратную данной. т.е:
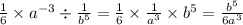
Система линейных уравнений с двумя неизвестными
x + y = 5
2x - 3y = 1
Система линейных ур-ний с тремя неизвестными
2*x = 2
5*y = 10
x + y + z = 3
Система дробно-рациональных уравнений
x + y = 3
1/x + 1/y = 2/5
Система четырёх уравнений
x1 + 2x2 + 3x3 - 2x4 = 1
2x1 - x2 - 2x3 - 3x4 = 2
3x1 + 2x2 - x3 + 2x4 = -5
2x1 - 3x2 + 2x3 + x4 = 11
Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100
3x + 5y + 7z + 9v = 116
3x - 5y + 7z - 9v = -40
-2x + 4y - 6z + 8v = 36
Система трёх нелинейных ур-ний, содержащая квадрат и дробь
2/x = 11
x - 3*z^2 = 0
2/7*x + y - z = -3
Система двух ур-ний, содержащая куб (3-ю степень)
x = y^3
x*y = -5
Система ур-ний c квадратным корнем
x + y - sqrt(x*y) = 5
2*x*y = 3
Система тригонометрических ур-ний
x + y = 5*pi/2
sin(x) + cos(2y) = -1
Система показательных и логарифмических уравнений
y - log(x)/log(3) = 1
x^y = 3^12
Объяснение:
Тип 2 в3× 4в5= 8в8