Линейная функция имеет вид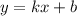 
. Раз известно, что точка А(1,5; -2) принадлежит графику, и учитывая то, что координаты точки задаются как (x;y), мы можем найти коэффициент b. У нас k=1/2 по условию. Далее мы вместо y подставляем -2, а вместо x -> 1,5.
-2=(1/2)*1,5+b;
b=-2-0,75=-2,75.
Теперь у нас изветстно всё, чтобы записать уравнение графика.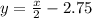
.
У параллельных прямых угловой коэффициент одинаковый.
Уравнение параллельной прямой для данной будет иметь вид: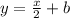 
Так же подставляем вместо x и y координаты точки, чтобы найти b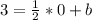
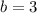. Уравнение прямой, проходящей через точку (0;3): 
.
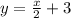Решение можно сократить, если помнить, что коэффициент b как раз определяет точку пересечения с осью ординат.
Объяснение:
Объяснение:
1. Дана функция: у = х² - 4х - 5 ;
a) запишите координаты вершины параболы;
Формула: х₀ = -b/2a
x₀ = 4/2 = 2;
y₀ = 2² - 4*2 - 5 = 4 - 8 - 5 = -9.
Координаты вершины параболы (2; -9).
b) запишите ось симметрии параболы;
x = 2;
c) найдите точки пересечения графика с
осями координат;
1) при пересечении графиком оси Оу х равен
нулю:
у = х² - 4х - 5 ; х = 0
у = 0² -4*0 - 5 = -5;
Координаты пересечения графиком оси Оу
(0; -5);
2) при пересечении графиком оси Ох у равен
нулю:
у = х² - 4х - 5 ; у = 0
х² - 4х - 5 = 0, квадратное уравнение, ищем
корни:
D=b²-4ac =16 + 20 = 36 √D= 6
х₁=(-b-√D)/2a
х₁=(4-6)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(4+6)/2
х₂=10/2
х₂=5.
Координаты пересечения параболой оси Ох
(-1; 0); (5; 0).
d) постройте график функции.
График - парабола со смещённым центром,
ветви направлены вверх.
Таблица
х -3 -2 -1 0 1 2 3 4 5 6 7
у 16 7 0 -5 -8 -9 -8 -5 0 7 16
График прилагается.
e) найдите промежутки убывания и
возрастания функции;
Функция возрастает при х∈(2; +∞);
Функция убывает при х∈(-∞; 2).
2. Дана функция у = -3х² - 5х - 2.
а) Найдите значения функции f(2), f(−1).
Подставить в уравнение значение х и
вычислить значение у:
1) у = -3х² - 5х - 2 х=2
у = -3 * 2² - 5*2 - 2 = -12 -10 - 2 = -24;
f(2) = -24.
2) у = -3х² - 5х - 2 х= -1
у = -3 * (-1)² - 5*(-1) - 2 = -3 + 5 - 2 = 0
f(−1) = 0.
b) Известно, что график функции проходит
через точку ( k ; 0). Найдите значение k.
у = -3х² - 5х - 2 х=k у=0
-3k² - 5k - 2 = 0/-1
3k² + 5k + 2 = 0, квадратное уравнение, ищем
корни:
D=b²-4ac =25 - 24 = 1 √D= 1
k₁=(-b-√D)/2a
k₁=(-5-1)/6
k₁= -6/6
k₁= -1;
k₂=(-b+√D)/2a
k₂=(-5+1)/6
k₂= -4/6
k₂= -2/3.
3. Дана функция у = 2х² − 8x + 7.
Не строя графика, найдите:
а) область определения функции.
1) Область определения функции - это
значения х, при которых функция существует.
Так как график квадратичной функции
парабола, область её определения ничем не
ограничен.
Область определения функции D(y) = х∈R,
множество всех действительных чисел, или
D(y) = х∈(-∞; +∞).
b) наименьшее значение функции.
Наименьшее и наибольшее значение функции
определяется ординатой вершины параболы
в зависимости от направления её ветвей.
В данном примере ветви параболы
направлены вверх, значит, наименьшим
значением функции будет ордината вершины
(у₀).
у = 2х² − 8x + 7
Х гривен вкладчик положил на 8% годовых,
2000 -Х гривен вкладчик положил на 10% годовых,
(Х х 100)/8 гривен вкладчик получил проценты с 8% счета,
(2000 -Х)х100/10 гривен вкладчик получил проценты с 10% счета
(Х х 100)/8 + (2000 -Х)х100/10 =176
0,08Х + (2000-Х) х 0,1=176
0,08Х + 200 -0,1Х = 176
-0,02Х = - 24
Х = 1200
2000 - 1200 = 800
ответ: 1200 гривен вкладчик положил на 8% годовых,
800 гривен вкладчик положил на 10% годовых