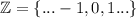
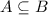и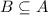 
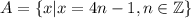
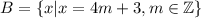
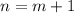
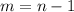
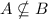то,значит, есть такой элемент 
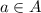так что 
.
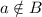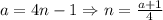
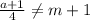
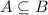
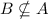, то значит есть такой элемент 
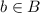так что: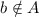 
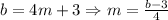
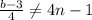
10 (км/час) - скорость катера в стоячей воде
Объяснение:
х - скорость катера в стоячей воде
х+2 - скорость катера по течению
х-2 - скорость катера против течения
Сейчас определимся со временем:
вышел в 13.00, вернулся в 19.30, был в пути 6,5 часов.
Но 2 часа 45 минут он ждал, это 2 и 45/60=2,75 часа.
Значит, в пути катер находился 6,5-2,75=3,75 часа, уравнение:
18/(х+2) - время по течению
18/(х-2) - время против течения
18/(х+2)+18/(х-2)=3,75 Избавляемся от дробного выражения, общий знаменатель (х+2)(х-2) или х²-4, надписываем над числителями дополнительные множители:
18(х-2)+18(х+2)=3,75(х²-4)
18х-36+18х+36=3,75х²-15
-3,75х²+36х+15=0
3,75х²-36х-15=0/3,75
х²-9,6х-4=0
х₁,₂=(9,6±√92,16+16)/2
х₁,₂=(9,6±√108,16)/2
х₁,₂=(9,6±10,4)/2
х₁= -0,4 отбрасываем, как отрицательный
х₂= 10 (км/час) - скорость катера в стоячей воде
Проверка:
18 : 12=1,5 (часа) - время по течению
18 : 8=2,25 (часа) - время против течения
1,5+2,25+2,75 (остановка)=6,5 (часа) в пути, всё верно.
Объяснение:
4а) 3x³y³ + 3x²y⁴ - 6xy² = 3xy²(x²y + xy² - 2)
4б) 2a + a² - b² - 2b = a² - b² + 2a - 2b = (a - b)(a + b) + 2(a - b)
5. x - скорость велосипедиста
x + 28 - скорость мотоциклиста
x+ 0,5(x+28) = 32
x + 0,5x + 14 = 32
1,5x = 18
x = 12 км/ч - скорость велосипедиста.
х + 28 = 12 км/ч + 28 км/ч = 40 км/ч - скорость мотоциклиста.
Проверка:
Смоделируем ситуацию - велосипедист выезжает и за час проезжает 12 км. Через полчаса после его выезда, выезжает мотоциклист и со скоростью 40 км/ч преодолевает 20 км за полчаса.
12 км + 20 км = 32 км (что означает, что задачу мы решили совершенно правильно).