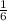2.представьте в виде степени с основанием x выражение: 1). (x⁵)²· (x² ·x )⁴ ; 2).· ; 3))⁴ · )⁵꞉ (-x³· x⁷)³.

👇

Увидеть ответ

Ответ:

lizasolnce2004

29.05.2020

1). (x⁵)²· (x² ·x )⁴=х¹⁰*х⁸*х⁴=х²² ;

5) (-x³· x⁷)³=-х⁹*х²¹=-х³⁰.

4,6(52 оценок)

Открыть все ответы

Ответ:

Цветочек123огрл

29.05.2020

y=16-8x+ln(4x)+ln2
У этой функции очень близкие значения от аргументов 1/9 и 2/15:
1/9 2/15
х = 0,111111 0,133333
у = 14,99333 14,99787
Максимальное значение у= 15 при х = 1/8.
Область определения функции. ОДЗ: x > 0
Точка пересечения графика функции с осью координат Y: График пересекает ось Y, когда x равняется 0: подставляем x=0 в 16-8*x+ln(4*x)+ln(2).
Результат: y=zoo. Точка: (0, zoo) Точки пересечения графика функции с осью координат X: График функции пересекает ось X при y=0, значит нам надо решить уравнение: 16-8*x+ln(4*x)+ln(2) = 0 Решаем это уравнение и его корни будут точками пересечения с X:
x=-LambertW(-exp(-16))/8. Точка: (-LambertW(-exp(-16))/8, 0) Экстремумы функции: Для того, чтобы найти экстремумы, нужно решить уравнение y'=0 (производная равна нулю), и корни этого уравнения будут экстремумами данной функции: y'=-8 + 1/x=0
Решаем это уравнение и его корни будут экстремумами: x=1/8. Точка: (1/8, 15) Интервалы возрастания и убывания функции: Найдем интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим на ведет себя функция в экстремумах при малейшем отклонении от экстремума: Минимумов у функции нету Максимумы функции в точках: 1/8 Возрастает на промежутках: (-oo, 1/8] Убывает на промежутках: [1/8, oo) Точки перегибов графика функции: Найдем точки перегибов для функции, для этого надо решить уравнение y''=0 - вторая производная равняется нулю, корни полученного уравнения будут точками перегибов указанного графика функции,
+ нужно подсчитать пределы y'' при аргументе, стремящемся к точкам неопределенности функции: y''=-1/x^2=0
Решаем это уравнение и его корни будут точками, где у графика перегибы.
Вертикальные асимптоты Нету
Горизонтальные асимптоты графика функции: Горизонтальную асимптоту найдем с предела данной функции при x->+oo и x->-oo. Соотвествующие пределы находим : lim 16-8*x+ln(4*x)+ln(2), x->+oo = -oo, значит горизонтальной асимптоты справа не существуетlim 16-8*x+ln(4*x)+ln(2), x->-oo = oo, значит горизонтальной асимптоты слева не существует Наклонные асимптоты графика функции: Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при x->+oo и x->-oo. Находим пределы : lim 16-8*x+ln(4*x)+ln(2)/x, x->+oo = -8, значит уравнение наклонной асимптоты справа: y=-8*xlim 16-8*x+ln(4*x)+ln(2)/x, x->-oo = -8, значит уравнение наклонной асимптоты слева: y=-8*x Четность и нечетность функции: Проверим функци четна или нечетна с соотношений f(x)=f(-x) и f(x)=-f(x). Итак, проверяем: 16-8*x+ln(4*x)+ln(2) = 8*x + ln(-4*x) + ln(2) + 16 - Нет16-8*x+ln(4*x)+n(2) = -(8*x + ln(-4*x) + ln(2) + 16) - Нет значит, функция не является ни четной ни нечетной.

4,8(73 оценок)

Ответ:

Meager36655

29.05.2020

Итак, у нас в любом случае a, b и с будут положительными от 1 до 6.
$D= b^{2}-4ac \geq 0 = b^{2} \geq 4ac$
b точно не может быть 1.
а) Рассмотрим случай, когда b = 2, вероятность такого события равна $\frac{1}{6}$ . Тогда произведение ac должно быть 1, вероятность такого исхода 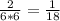$\frac{2}{6*6}= \frac{1}{18}$ Общая вероятность этих двух событий равна произведению вероятностей, ибо эти два события независимые: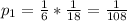
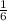$p_{1}= \frac{1}{6}* \frac{1}{18}= \frac{1}{108}$
б) b = 3, вероятность этого $\frac{1}{6}$ . Тогда произведение ас должно быть не больше двух, благоприятных исходов 4 из 36, вероятность такого события 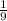$\frac{1}{9}$ Общая вероятность этих двух событий равна произведению вероятностей, ибо эти два события независимые: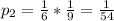
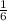$p_{2}= \frac{1}{6}* \frac{1}{9}= \frac{1}{54}$
в) b = 4, вероятность этого $\frac{1}{6}$ . Тогда произведение ас должно быть не больше четырех, благоприятных исходов 8 из 36, вероятность такого события 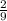$\frac{2}{9}$ Общая вероятность этих двух событий равна произведению вероятностей, ибо эти два события независимые: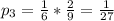
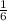$p_{3}= \frac{1}{6}* \frac{2}{9}= \frac{1}{27}$
г) b = 5, вероятность этого $\frac{1}{6}$ . Тогда произведение ас должно быть не больше шести, благоприятных исходов 16 из 36, вероятность такого события 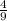$\frac{4}{9}$ Общая вероятность этих двух событий равна произведению вероятностей, ибо эти два события независимые: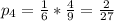
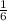$p_{4}= \frac{1}{6}* \frac{4}{9}= \frac{2}{27}$
д) b = 6, вероятность этого $\frac{1}{6}$ . Тогда произведение ас должно быть не больше девяти, благоприятных исходов 20 из 36, вероятность такого события 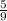$\frac{5}{9}$ Общая вероятность этих двух событий равна произведению вероятностей, ибо эти два события независимые: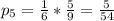
$p_{5}= \frac{1}{6}* \frac{5}{9}= \frac{5}{54}$
Чтобы получить общую вероятность, нам надо сложить полученные вероятности, ибо события зависимые:
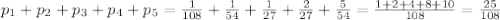
$p_{1}+p_{2}+p_{3}+p_{4}+p_{5}=\frac{1}{108}+\frac{1}{54}+\frac{1}{27}+ \frac{2}{27}+ \frac{5}{54}=\frac{1+2+4+8+10}{108}=\frac{25}{108}$