Объяснение:
Пользуясь тем, что 1,4<√2<1,5 и 2,4<√6<2,6 оцените:
а) √24+ √2
б) √18+ √6
a)√24+ √2
√24=√2·√2·√6
1,4·1,4·2,4 < √2·√2·√6 < 1,5·1,5·2,6
1,4·1,4·2,4 + 1,4 < √2·√2·√6 + √2 < 1,5·1,5·2,6 + 1,5
4,704 + 1,4 < √24 + √2 < 5,85 + 1 ,5
6,104 < √24 + √2 < 7,35
б) √18+ √6
√18=√(36:2)=6/√2
1,4<√2<1,5
14/10<√2<15/10
10/15<1/√2<10/14 умножим на 6
60/15<6/√2<60/14
4 < 6/√2 < 30/7
30/7≈4,29
4 +√6 < 6/√2 + √6 < 30/7 + √6
4 + 2,4 < √18 + √6 < 30/7 + 2,6
6,4 < √18 + √6 < 4,29 +2,6
6,4 < √18 + √6 < 6,89
Объяснение:
1. 2x-3y=-7; [*(-3)]
3x-2y=-8; [*2]
------------
-6x+9y=21; (1)
6x-4y=-16; (2)
------------------
Складываем (1) и (2)
9y-4y=21-16;
5y=5;
y=1.
-----------
Подставим в исходное:
2x-3*1=-7;
2x=-7+3;
2x=-4
x= -2.
***
2. x-3y=-4; (1)
5x-3y=-8; (2)
-----------------
Из (1) x=-4+3y;
Подставим в (2):
5(-4+3y)-3y=-8;
-20+15y-3y=-8;
15y-3y=-8+20;
12y=12;
y=1.
------------
y=1 подставим в (1)
x-3*1=-4;
x=-4+3;
x=-1.
***
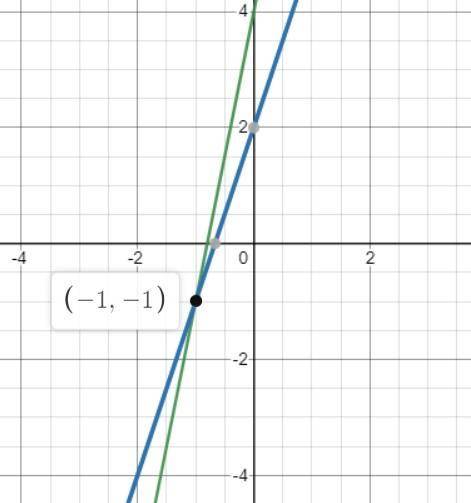
3. y=3x+2 ;
y-5x=4.
-------------------
Решаем графически. Смотрите скриншот.
3x^2 + 6x + 3 = 2x + 2
3x^2 + 4x + 1 = 0
D = 4^2 - 4 * 3 * 1 = 16 - 12 = 4
√D = √4 = 2
x1 = (-4 + 2) / 6 = -2 / 6 = - 1/3
x2 = (-4 - 2) / 6 = - 6 / 6 = -1
ответ: -1.
(x + 3)(x - 1) = 2x(x - 2) + 5
...
x^2 - 6x + 8 = 0
D = 6^2 - 4*1*8 = 36 - 32 = 4
√D = √4 = 2
x1 = (6 + 2) / 2 = 8 / 2 = 4
x2 = (6 - 2) / 2 = 4 / 2 = 2
ответ: 2.