1) c² + b³ - cb + c - cb² - b² = (c² - cb + c) + (b³ - cb² - b²) =
= c(c - b + 1) + b²(b - c - 1) = c(c - b + 1) - b²( c - b + 1) = (c - b + 1)(c - b²)
2) (x + y - 7)² + (x - 2y + 2)² = 0
Это равенство верно только в случае, когда :
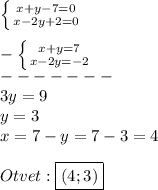
3) Пусть надо взять х кг 25% - го и y кг 50% - го сплавов меди . Надо получить 20 кг 40% - го сплава.
x y 20 = x + y
25% 50% 40%
0,25x + 0,5y = 0,4(x + y)
Если x + y = 20 , то y = 20 - x
0,25x + 0,5 * (20 - x) = 0,4 * 20
0,25x + 10 - 0,5x = 8
- 0,25x = - 2
x = 8 кг - 25% - го
y = 20 - 8 = 12 кг - 50% - го
ответ : надо взять 8 кг 25% - го и 12 кг 50% - го сплавов
ответ:Для того, чтобы представить выражение 4x^2 + y^2 + 4xy в виде квадрата двучлена мы применим формулу сокращенного умножения квадрат суммы.
Итак, вспомним прежде всего формулу квадрат суммы:
(a + b)^2 = a^2 + 2ab + b^2.
Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого выражения на второе, плюс квадрат второго выражения.
Но прежде чем применить формулу преобразуем выражение к виду:
4x^2 + y^2 + 4xy = 4x^2 + 4xy + y^2 = (2x)^2 + 2 * 2x * y + y^2 = (2x + y)^2.
Объяснение:
7х=35
х= 5
1 сторона 15 см
2 сторона 5 см
3 сторона 14 см