Возрастающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)Убывающая функция- если для любых х1 и х2, таких, что х1< х2, выполняется неравенство f(х1)>f(х2) Если k>0, то функция убывает на промежутке (0;+Y) и на промежутке (-Y;0). Если k<0, то функция возрастает на промежутке (-Y;0) и на промежутке (0;+Y). Графиком функции является гипербола. F(x) = k/x k = 1; x1=1; x2=2 f(1)=1/1 = 1 f(2) = 1/2 = 0.5 f(1) > f(2) k = -1; x1=-1; x2=-2 f(-1)=-1/1 = -1 f(-2) = -1/2 = -0.5 f(-1)< f(-2)
Разберем по частям, начнем с простого: Квадратный корень из 81 естественно равен 9: √81=9; Далее разберемся с первым числом, имеем: Знаменатель в степени числа всегда показывает какой у нас корень, в данном случае - корень квадратный, а квадратный корень, как известно записывается так: Следовательно, у нас идет квадратный корень из девяти в кубе: Квадратный корень из 729 извлекается, это 27. Теперь второе число: В знаменателе степени стоит 3, то есть, корень кубический. Выглядит так: То бишь, если квадратный корень из 729 равен 27, то теперь из 27 находим квадратный корень, чтобы найти кубический корень из 729. Получаем 9. В итоге, складывая: 27+9+9=45.
Наименьшее значение функции будет при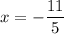
равное 0
ответ: 0