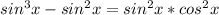
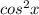 как
как 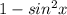 (исходя из основного тригонометрического тождества
(исходя из основного тригонометрического тождества 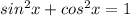 )
)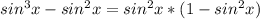
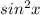 ) =
) = 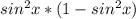
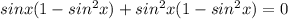
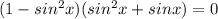
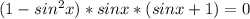
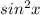 = 0
= 0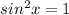
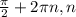 ∈ Z
∈ Z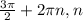 ∈ Z
∈ Z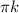 , k ∈ Z
, k ∈ Z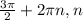 ∈ Z
∈ Z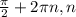 ∈ Z
∈ Z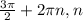 ∈ Z
∈ Z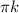 , k ∈ Z
, k ∈ Z
Некоторые формулы расчетов знакомы каждому школьнику. Например, если нужно уточнить диаметр конкретной трубы, следует измерить ее окружность. Для этого можно воспользоваться сантиметровой лентой, которой пользуются швеи. Или же следует обернуть трубу другой подходящей лентой, а затем измерить полученный отрезок с линейки.
Далее используем формулу длины окружности:
L=πD, где:
L — длина окружности круга;π — постоянное число «пи», равное примерно 3,14;D — диаметр окружности круга.Достаточно проделать несложное преобразование, чтобы вычислить с этой формулы внешний диаметр трубы:
D=L/π.
Измерив толщину стенок трубы, легко рассчитать также внутренний диаметр круга. Для этого от значения внешнего диаметра трубы следует отнять удвоенное значение толщины стенок трубы.
7ⁿ · 2³ⁿ - 3²ⁿ =
= 7ⁿ · (2³)ⁿ - (3²)ⁿ =
= 7ⁿ · 8ⁿ - 9ⁿ =
= (7 · 8)ⁿ - 9ⁿ =
= 56ⁿ - 9ⁿ
Для полученного выражения (56ⁿ - 9ⁿ) применим формулу сокращённого умножения для n-ой степени:
aⁿ - bⁿ = (a - b)((aⁿ⁻¹+aⁿ⁻² b+aⁿ⁻³b²+ ...+ a²bⁿ⁻³+a bⁿ⁻²+ bⁿ⁻¹)
Разложим (56ⁿ - 9ⁿ) на множители:
56ⁿ - 9ⁿ =
= (56-9)(56ⁿ⁻¹+56ⁿ⁻²·9+56ⁿ⁻³·9²+...+56²·9ⁿ⁻³+56·9ⁿ⁻²+9ⁿ⁻¹) =
= 47 · (56ⁿ⁻¹+56ⁿ⁻²*9+56ⁿ⁻³*9²+...+56²*9ⁿ⁻³+56*9ⁿ⁻²+9ⁿ⁻¹).
Один из сомножителей делится на 47, значит и все произведение делится на 47, что и требовалось доказать.