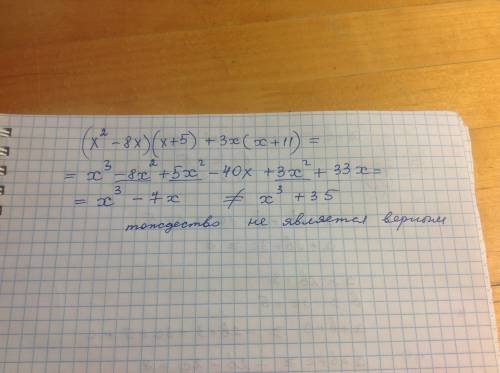
Решение. Каждое из уравнений системы является линейным уравнением с двумя неизвестными. Нам известно, что графиком такого уравнения является прямая. Построим графики этих уравнений в одной системе координат.
Как мы видим, графики этих прямых пересекаются в точке с координатами . Что дает нам этот факт? Дело в том, что если точка принадлежит графику уравнения, то ее координаты удовлетворяют этому уравнению, то есть обращают его в верное числовое равенство. Так как точка пересечения одновременно принадлежит двум графикам уравнений, то ее координаты удовлетворяют одновременно обоим уравнениям, то есть координаты этой точки являются решением системы уравнений.
Мы использовали так называемый графический решения системы уравнений.
Дано -a^2+4a-9. Вынесем знак "-" за скобки и получим -(a^2-4a+9). Выражение в скобках представим в виде квадрата разности двух чисел (a-b)^2=a^2-2ab+b^2, тогда оно будет иметь следующий вид: a^2-4a+ 4 +5 или (a-2)^2 + 5. Очевидно, что указанное выражение всегда имеет положительное значение так как представляет собой сумму двух положительных чисел (а-2)^2 (квадрат любого числа всегда положителен) и "5". Но по условиям задачи перед выражением (a-2)^2 + 5 стоит знак "-", следовательно все значения данного выражения будут отрицательными.
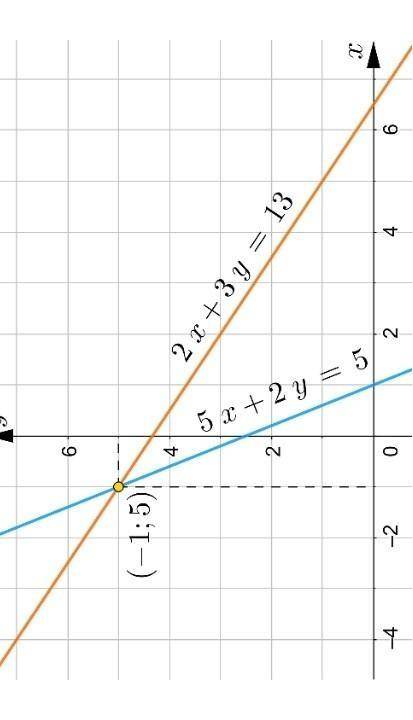
Тождество не является верным. Здесь даже без решения ясно, что 35 никак не может получиться, так как все выражения содержат Х.