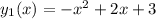 (1)
(1)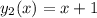 (2)
(2)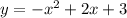 (1)
(1)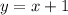 (2)
(2)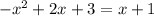
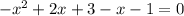
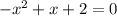 (3)
(3)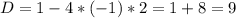
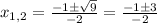
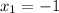
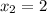
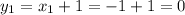
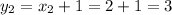
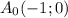

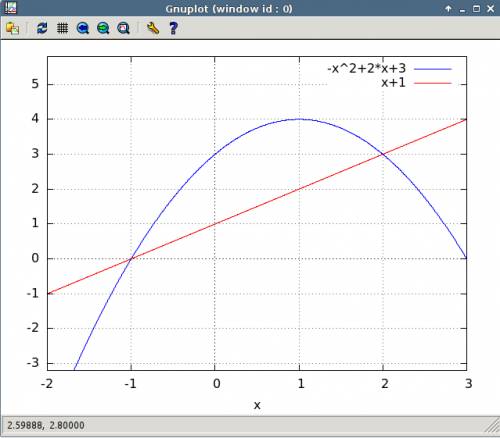
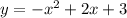 в параболу
в параболу  .
.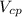 будет равен:
будет равен: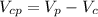 (4)
(4)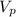 объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую
объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую 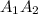 .
.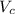 ? , объем конуса ограниченного прямыми и той же плоскостью проходящей через
? , объем конуса ограниченного прямыми и той же плоскостью проходящей через 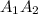
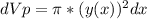
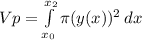 (5)
(5)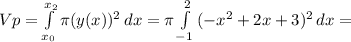
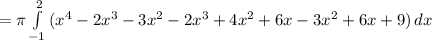
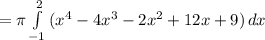 (6)
(6)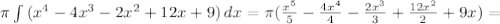
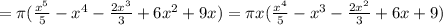 (7)
(7)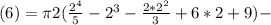
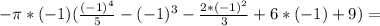
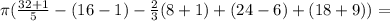
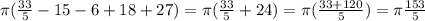 (8)
(8)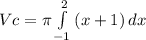 (9)
(9)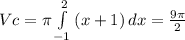 (10)
(10)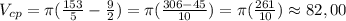
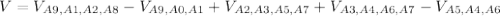
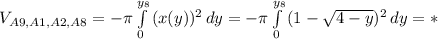
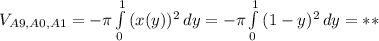

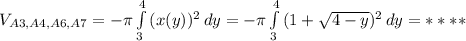

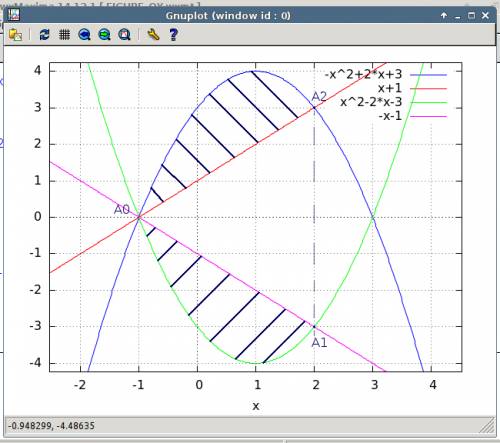
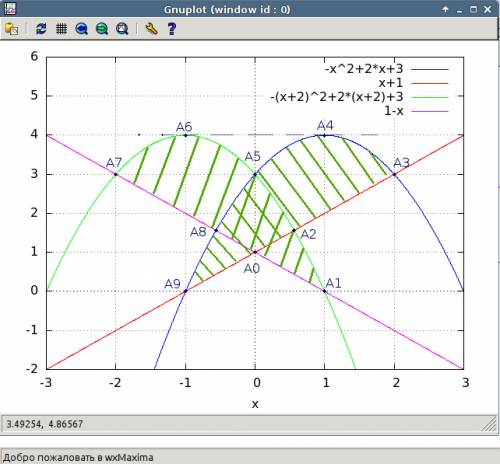
В решении.
Объяснение:
а) 0,6х²у * ? = -3х⁴у
? = - 3х⁴у / 0,6х²у =
3 и 0,6 сократить (разделить) на 0,6; х⁴ и х² на х²; у и у на у:
= - 5х²;
б) ? * (-4ху²) = 8,2х³у³
? = 8,2х³у³ / (-4ху²)=
сократить (разделить) 8,2 и 4 на 4; х³ и х на х; у³ и у² на у²:
= -2,05х²у;
в) -5ху * ? = 0,8х²у³
? = 0,8х²у³ / (-5ху)=
сократить (разделить) 0,8 и 5 на 5; х² и х на х; у³ и у на у:
= -0,16ху².
Проверка путём подстановки вычисленных значений неизвестной величины в выражения показала, что данные решения удовлетворяют данным выражениям.
/ - знак деления.
D=b²-4ac
D=0,25-16
D<0 => нет корней
ответ: нет корней