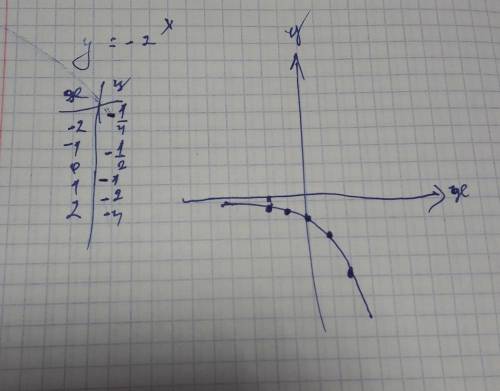
Объяснение:
x²-36=0;
x²=36;
x=±6.
***
2x²-3x=0;
x(2x-3)=0;
x1=0;
2x=3;
x=3/2;
x2=1.5.
***
4x²-x=3x-1;
4x²-4x+1=0;
a=4; b=-4; c=1;
D=b²-4ac=(-4)²-4*4*1=16-16=0 - два равных корня.
х1=x2=(-b)/2a=(-(-4))/2*4=4/8=1/2=0.5.
***
6x²+9x-2x-3=6x-3;
6x²+x=0;
x(6x+1)=0;
x1=0;
6x=-1;
x2= - 1/6.
***
12x+18-2x²-12x-12=0;
-2x²+6=0;
x²=3;
x1,2=±√3
***
(3x-1)² - (x+2)²=15;
9x²-6x+1 - x²-4x-4-15=0;
8x²-10x-18=0; [: 2]
4x²-5x-9=0;
a=4; b=-5; c=-9;
D=b²-4ac=(-5)²-4*4*(-9)=25+144=169=13² >0 0 - два корня.
x1=(-b+√D)/2a=(-(-5)+13)/2*4=(5+13)/8 =18/8=2.25;
x2=(-b-√D)/2a=(-(-5)-13)/2*4=-8/8= -1.
***
a=3; b=-5; c=(-a+9);
D=b²-4ac=(-5)²-4*3*(-a+9)=25+12a-108=12a-83;
12a-83<0;
12a=83;
a=83/12
a=6 11/12;
При a<6 11/12 D<0 - нет корней.
***
???
В решении.
Объяснение:
Для линейной функции
1) y=8x - 1
2) y=3 - 4x
3) y= - 2+2x
запишите формулу такой линейной функции, график которой:
а)параллелен графику данной функции ;
б)пересекает график данной функции ;
в)совпадает с графиком данной функции.
Теория:
1) Если k₁ = k₂, b₁ ≠ b₂ прямые будут параллельны;
2) Если k₁ ≠ k₂, прямые пересекутся.
3) Если k₁ = k₂, b₁ = b₂ прямые совпадут;
1) y=8x - 1
а)у=8х + 5
б)у=3х - 4
в)16х - 2у = 2
После преобразований:
-2у = 2 - 16х
2у = 16х - 2
у = 8х - 1.
2) y=3 - 4x
а)у= 10 - 4х
б)у=5х + 2
в)8х + 2у = 6
После преобразований:
2у= 6 - 8х
у=3 - 4х.
3) y= - 2 + 2x
а) у=2х + 7
б) у=3х + 4
в) 6 + 3у = 6х
После преобразований:
3у = 6х - 6
у = 2х - 2.