1) После преобразования получена дробь:
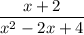
2) Значение полученной дроби при х = -2 равно нулю.
Объяснение:
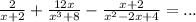
Если заметить, что 8 = 2³, а 4 = 2², то напрашивается использование формулы суммы кубов:
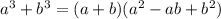
для приведения всех дробей к единому знаменателю.
Домножим у каждой дроби числитель и знаменатель на недостающие множители:
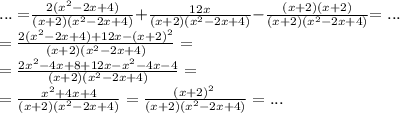
После сокращения мы получаем вполне "красивую" дробь:
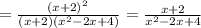
Однако - стоит отметить, что строго говоря, данная дробь не равносильна исходной.
При сокращении мы убрали из знаменателя множитель (х+2), поэтому, несмотря на то, что полученное в конце выражение при х=-2 имеет вполне конкретное и определенное значение,
(!) при х = -2 исходное выражение не определено, что обязательно нужно указать и учитывать при сокращении дробей!
Однако нас просят найти значение полученной дроби, что вполне реально. Итак:
при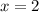 значение выражения
значение выражения 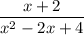 равно:
равно:
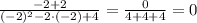
Итак, ответ:
1) После преобразования получена дробь:
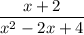
2) Значение полученной дроби при х = -2 равно нулю.
В решении.
Объяснение:
Решите уравнение.
7) х² + 4х = 5
↓
х² + 4х - 5 = 0
D=b²-4ac = 16 + 20 = 36 √D=6
х₁=(-b-√D)/2a
х₁=(-4-6)/2
х₁= -10/2
х₁= -5;
х₂=(-b+√D)/2a
х₂=(-4+6)/2
х₂=2/2
х₂= 1; В ответе х = -5;
8) х² - 6х = 16
↓
х² - 6х - 16 = 0
D=b²-4ac = 36 + 64 = 100 √D=10
х₁=(-b-√D)/2a
х₁=(6-10)/2
х₁= -4/2
х₁= -2;
х₂=(-b+√D)/2a
х₂=(6+10)/2
х₂=16/2
х₂= 8; В ответе х= -2;
9) х² + 2х = 15
↓
х² + 2х - 15 = 0
D=b²-4ac = 4 + 60 = 64 √D=8
х₁=(-b-√D)/2a
х₁=(-2-8)/2
х₁= -10/2
х₁= -5;
х₂=(-b+√D)/2a
х₂=(-2+8)/2
х₂=6/2
х₂= 3; В ответе х = -5;
10) х² - 7х = 8
↓
х² - 7х - 8 = 0
D=b²-4ac = 49 + 32 = 81 √D=9
х₁=(-b-√D)/2a
х₁=(7-9)/2
х₁= -2/2
х₁= -1;
х₂=(-b+√D)/2a
х₂=(7+9)/2
х₂=16/2
х₂= 8; В ответе х = -1.

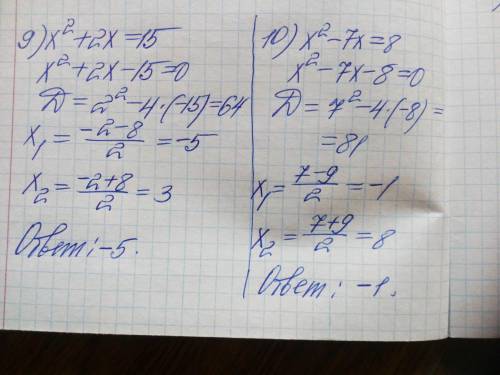
A2=21.4
d=a2-a1=21.4-22.7= -1.3
a1/|d| =22.7/1.3= 17,46...
17.46>17
An=A1+D(n-1)
Где n-1=17
n=18
=> A18=22.7+(-1.3)*(18-1)=0.6
Так же стоит проверить 19 член, ведь если его модуль меньше модуля А19, то ответом будет являтся именно он.
A19=22.7+(-1.3)*(19-1)=-0.7
|A19|>|A18|
=> A18
ответ: Ближайший член к нулю A18, равный 0.6